统计学习方法
C1 统计学习方法概论
统计学习三要素:模型 + 策略(cost-function) + 算法.
交叉验证的基本想法是重复地使用数据:把给定的数据进行切分,将切分的数据集组合为训练集与测试集,在此基础上反复地进行训练测试以及模型选择。 1)简单交叉验证. 2)S折交叉验证(随机地将已给数据切分为S个互不相交的大小相同的子集,然后利用S-1个子集的数据训练模型,利用剩余1个子集测试模型。重复S次). 3)留一交叉验证(S=N的特殊情况,通常在数据缺乏的情况下使用)
监督学习可分为生成方法(generative approach)和判别方法(discriminative approach). 所学到的模型分别称为生成模型(generative model)和判别模型(discriminative approach).
- 生成方法学习联合概率分布P(X,Y),然后求解条件概率分布P(Y|X)=P(X,Y) / P(X)作为预测模型。之所以称为生成方法,是因为模型表示了给定输入X产生输出Y的生成关系。比如朴素贝叶斯和隐式马尔可夫模型。
- 判别方法直接学习决策函数f(X)或者P(Y|X), 关心给定输入X应该预测什么样的输出Y。比如kNN, 感知机,决策树,逻辑回归,最大熵,SVM,提升模型和条件随机场等。
标注问题(tagging)输入是一个观测序列,输出式一个标记序列或状态序列。标注问题的目的在于学习一个模型,使它能够对观测序列给出标记序列作为预测。评价标注模型的指标与评价分类模型的指标一样,常用的有标注准确率,精确率和召回率。常用的统计学习方法有:隐式马尔可夫模型,条件随机场。
C2 感知机
- 感知机(perceptron)是二类分类的线性分类模型, 对应于在输入空间(特征空间)中将实例划分为正负两类的分离超平面, 属于判别模型.
- 感知机学习旨在求出将训练数据进行线性划分的分离超平面, 学习算法分为原始形式和对偶形式. 感知机是神经网络与支持向量机的基础.
- 如果训练数据是线性可分时, 感知机算法迭代是收敛的. 当训练数据线性不可分时, 感知机学习算法不收敛, 迭代结果会发生震荡.
- 感知机学习算法存在许多解, 这些解既依赖于初值的选择, 也依赖于迭代过程中误分类点的选择顺序. 为了得到唯一的超平面, 需要对分类超平面增加约束条件, 这就是SVM的想法.
C3 kNN
KNN三要素: 距离度量, k值选择和分类决策规则.
- 常用的距离度量是欧式距离以及更一般的Lp距离. (Minkowski距离 Lp(x,y) = (\SUM (x(i) - y(i)) ^ p) ^ (1/p))
- k值小时, 就相当于用较小领域中的训练实例进行预测. "学习"的近似误差(approximation error)会减小, 只有与输入实例较近的(相似的)训练实例才会对预测结果起作用. 但缺点是"学习"的估计误差(estimation error)会增大, 预测结果会对近邻的实例点非常敏感. 如果近邻的实例点恰好是噪声, 预测就会出错. 换句话说, k值的减小就意味着整体模型变得更加复杂, 容易发生过拟合.
- k值大时, 就相当于用较大领域中的训练实例进行预测. 优点是可以减少学习的估计误差. 但缺点是学习的近似误差会增大. 这时与输入实例较远(不相似的)的训练实例也会对预测其作用, 使预测发生错误. k值的增大就意味着整体模型的变得简单.
- 常用的分类决策规则是多数表决, 对应于经验风险最小化.
kNN的实现需要考虑如何快速搜索k个最邻近点. kd树是一种便于对k维空间中的数据进行快速检索的数据结构. kd树是二叉树, 表示对k维空间的一个划分, 其每个节点对应于k维空间划分中的一个超矩形区域. 利用kd树可以省去对大部分数据点的搜索, 从而减少搜索的计算量.
C4 朴素贝叶斯
朴素贝叶斯方法他训练数据集学习联合概率分布P(X,Y). 具体地学习先验概率分布P(Y)以及条件概率分布P(X|Y). 然后根据联合概率分布选择后验概率最大的y. P(Y|X) = P(X,Y) / P(X).
条件概率分布P(X|Y)有指数量级的参数(因为X的组合), 所以难以估计实际概率. 朴素贝叶斯对条件概率分布做了条件独立性的假设: X的各个特征之间相互独立. 这样P(X|Y) = \PROD (P(X(i) | Y)).
我们通过极大似然来估计来先验概率以及条件概率. 比如先验概率P(Y=ck)的极大似然估计是# of ck in traning set / # of traning set. 条件概率P(X(i) | Y=ck) = # of (X(i), Y=ck) / # of (Y=ck).
但是上面的条件概率可能# of (Y=ck)会为0. 解决这一问题的方法是采用贝叶斯估计: 在分子上增加一个参数a, 分母上增加Z*a(Z为归一化参数). 如果a=0那么就是极大似然估计, 如果a=1那么就是拉普拉斯平滑(Laplace smoothing).
P(H(hypotheses) | E(evidence)) = P(H) * P(E/H) / P(E). 其中P(H)称为先验概率(prior probability), P(H/E)称为后验概率(post probability), P(E/H)称为证据似然值(likehood of evidence).
C5 决策树
决策树(decision tree)是一种基本的分类和回归方法. 它可以认为是if-then规则的集合, 也可以认为是定义在特征空间与类空间上的条件概率分布. 决策树学习通常包括3个步骤: 特征选择, 决策树的生成和决策树的修剪.
决策树学习的损失函数通常是正则化的极大似然函数. 决策树学习的策略是以损失函数为目标函数的最小化. 当损失函数确定之后, 学习问题就变为在损失函数意义下选择最优决策树的问题. 因为从所有可能的决策树中选取最优决策树是NP完全问题, 所以现实中决策树学习算法通常采用启发式方法, 近似求解这一最优化问题, 得到的决策树也是次最优(sub-optimal)的.
决策树学习算法通常是递归地选择最优特征, 根据该特征对训练数据进行分割, 使得对各个子数据集有一个最好的分类的过程. 这一过程对应着对特征空间的划分, 也对应着决策树的构建, 直到所有训练数据子集被正确分类. 这样构建好之后泛化能力会比较差, 可以通过剪枝去掉过分细分的叶子节点使其回退到父节点甚至更高的节点. 决策树的生成对应于模型的局部选择, 决策树的剪枝对英语模型的全局选择. 决策树的生成只考虑局部最优, 相对地, 决策树的剪枝则考虑全局最优.
特征选择可以通过信息增益或者是信息增益比来指导:
- 信息增益 g(D, A) = H(D) - H(D|A). 表示特征A对训练数据集合D的信息增益(互信息). 其中H(D)称为信息熵, 而H(D|A)称为条件熵. 因为我们是通过数据估计(贝叶斯估计, 或者是极大似然估计)来计算P的, 所以对应称为经验信息熵(empirical entropy)以及经验条件熵(empirical conditional entropy). ID3算法使用这个指标.
- 信息增益比 gR(D, A) = g(D, A) / H(D, A) 其中H(D, A)表示训练数据关于特征A的熵. 以信息增益作为划分训练数据集的特征, 存在偏向于选择取值比较多的特征的问题. 所以我们通过信息增益比来进行校正. C4.5算法使用这个指标.
决策树剪枝的损失函数定义为: 每个叶子节点上经验熵之和 + a * |T|(叶子数量). a可以控制模型复杂度: 较大a可以促使选择简单的模型树, 较小a可以促使选择比较复杂的模型树. 树的剪枝算法则是对比从某个节点剪枝前后损失函数大小, 如果损失函数变小的话那么就可以进行剪枝. 决策树的剪枝算法可以由在一种动态规划的算法实现.
CART(classification and regression tree)模型假设决策树是二叉树. CART既能够用于分类也能够用于回归, 对回归树选用平方误差最小准则, 对分类树使用基尼指数(Gini index)准则, 进行特征选择. 对于回归树每次选择特征, CART寻找最优切分变量(splitting variable)和切分点(splitting point), 以对应分类里面average-y为中心计算最小二乘, 使得这个最小二乘极小化. 而对于分类树准则, 类似选择最大信息增益(比), 只不过这里选择Gini index. Gini(p) = \SUM (p(k) - (1 - p(k))) = 1 - \SUM p(k) ^ 2. 其中k对于表示对应类. 我们选择的是Gini(D) - Gini(D, A)最大的特征. #note: CART剪枝有点复杂没有看懂.
C6 逻辑回归与最大熵模型
最大熵是概率模型学习的一个准则, 将其推广到分类问题得到最大熵模型(maximum entropy model). 逻辑回归与最大熵模型都是对数模型, 都是以似然函数为目标函数的最优化问题. 通常通过迭代算法求解. 从最优化的观点看, 这时的目标函数具有很好的性质: 它是光滑的凸函数, 因此多种最优化的方法都能使用, 且保证能够找到全局最优解. 常用的方法有改进的迭代尺度算法(improved iterative scaling, IIS), 梯度下降法, 牛顿法(newton method)和拟牛顿法(quasi newton method). 牛顿法和拟牛顿法一般收敛速度更快.
二项逻辑回归 vs. 多项逻辑回归。二项逻辑回归的似然函数是\PROD ((f(x) ^ y) * ((1 - f(x)) ^ (1-y))),为了方便计算取对数似然函数则是\SUM (y * log(f(x)) + (1-y) * log(1-f(x))) #note: 多项逻辑回归似然函数是什么?
最大熵原理认为, 学习概率模型时, 在所有可能的概率模型(分布)中, 熵最大的模型也是最好的模型. 通常用约束条件来确定概率模型的集合, 所以最大熵原理也可以表述为在满足约束条件的模型集合中选取熵最大的模型.
C7 支持向量机
支持向量机(SVM)是一种二类分类模型,它的基本模型是定义在特征空间上的间隔最大的线性分类器,间隔最大使它有别于感知机。支持向量机还包括核技巧,这使它称为实质上的非线性分类器。支持向量机学习策略就是间隔最大化,可以形式化为求解一个凸二次规划(convex quadratic programming)的问题,也等价于正则化的合页损失函数的最小化问题。序列最小最优化算法(sequential minimal optimization, SMO)是SVM学习的一种快速算法。
支持向量机学习方法包含构建由简至繁的模型,简单模型是复杂模型的基础,也是复杂模型的特殊情况:
- 线性可分支持向量机(linear support vector machine in linearly separable case). 线性完全可分,硬间隔最大化(hard margin maximization)
- 线性支持向量机(linear support vector machine). 线性近似可分,软间隔最大化(soft margin maximization)
- 非线性支持向量机(non-linear support vector machine). 线性不可分但是通过核技巧(kernel trick)可以软间隔最大化
当输入空间为欧式空间或离散集合,特征空间为希尔伯特空间时,核函数(kernel function)表示将输入空间映射到特征空间得到的特征向量之间的内积。通过使用核函数等价于隐式地在高维的特征空间中学习线性支持向量机。这样的方法称为核技巧。核方法(kernel method)是比支持向量机更为一般的机器学习方式。
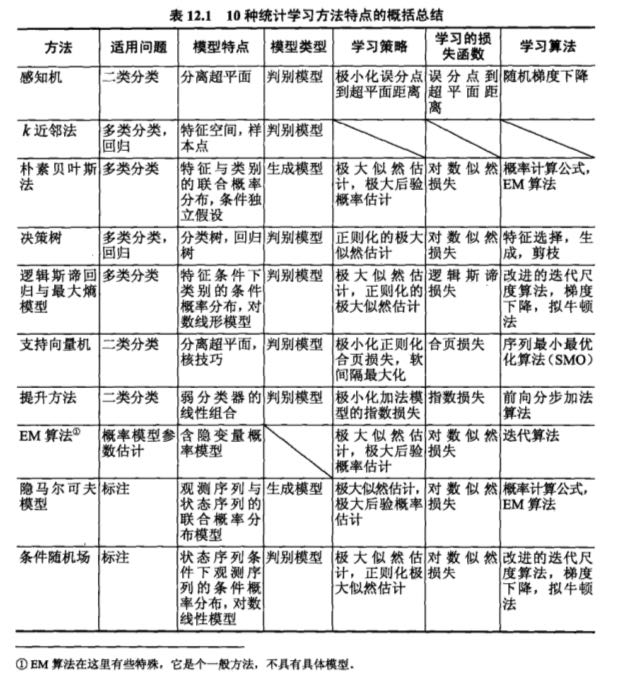
首先看线性可分支持向量机。我们得到(w,b)(法向量和截距)之后,可以定义分离超平面为wx+b=0. 因为我们是要确保间隔最大,训练数据集合的样本点中与分离超平面距离最近的样本点的实例称为支撑向量(support vector). 对于y=1的点,wx+b=1, 对于y=-1的点,wx+b=-1. 支撑向量距离超平面的距离为1/|w|. 图中H1, H2是间隔边界,上面所有点都是支撑向量,H1和H2之间的距离称为间隔(margin) = 2/|w|.
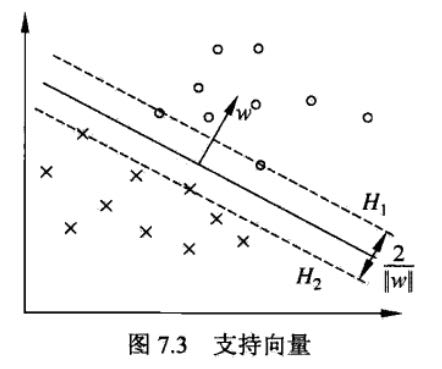
然后在看线性支持向量机。因为不是线性完全可分,所以引入松弛变量,然后在损失函数里面增加对松弛变量的惩罚。最终得到的是软间隔最大的分离超平面,不过这个超平面并不唯一,并且软间隔的支持向量可以在间隔边界上,也可以在超平面和间隔边界之间,也可以在误分的一侧。
学习的对偶算法里面可以发现,目标函数里面所有和输入相关的项,都转变称为了特征向量之间的内积。这就是为什么可以使用核函数的原因。核函数的定义是:假设X是输入空间,H为特征空间,如果存在一个X到H的映射f, 使得函数K(x1,x2)满足条件K(x1,x2) = f(x1) * f(x2)(内积). 则称K(x,y)为核函数,也称为正定核(positive definite kernel function)。核技巧的想法是:在学习与预测中只定义核函数K(x,y)而不显示定义映射函数f.
C8 提升方法
提升(boosting)方法是一种常用的统计学习方法,在分类问题中,它通过改变训练样本的权重,学习多个分类器,并将这些分类器进行线性组合,提高分类的性能。通常需要解决两个问题:1)每一轮如何改变训练数据的权值或者是概率分布 2)如何将弱分类器组合称一个强分类器。AdaBoost算法是比较有代表性的一个提升方法:在改变样本权重时,提高被错误分类样本的权值,降低被争取分类样本权值;在组合分类器时,加大分类误差率小的分类器的权值,而减小分类误差率大的分类器权值。提升树是以分类树或回归树为基本分类器的提升方法。
C9 EM算法及其推广
C10 隐马尔可夫模型
C11 条件随机场
C12 统计学习方法总结