Neural Networks for Machine Learning on Coursera

• 不同大脑皮层完成不同的工作，但是看上去却非常相似。这些大脑皮层都是由通用功能的东西组成的，但是在不断的学习中逐渐演变成为专用功能组件。
• 为了对事物建模，我们需要理想化它们：
  • 我们可以去除那些对于理解事物背后原理不相关的东西从而简化问题。
  • 我们可以与我们已经熟悉的系统进行类比并且将数学应用在上面。
  • 一旦我们了解背后原理我们就可以考虑增加复杂性来让模型更加符合事物。
  • 但是我们同时需要注意因为理想化导致这些模型有可能是错误的。
• neurons # 可能的神经元
  • binary threshold neurons
  • rectified linear neurons(ReLU, max(0, x))
  • sigmoid neurons # nice derivatives
  • stochastic binary neurons # use sigmoid value as probability to produce spike
• Reinforcement learning # 强化学习
  • In reinforcement learning, the output is an action or sequence of actions and the only supervisory signal is an occasional scalar reward. # 强化学习输出是一系列动作，偶尔会有监督信号以标量形式返回
    • The goal in selecting each action is to maximize the expected sum of the future rewards. # 我们选择每个动作是为了最大化未来奖励总和
    • We usually use a discount factor for delayed rewards so that we don’t have to look too far into the future. # 我们也会对延迟时间比较长的反馈给予discount，因为我们不想考虑得过于长远
  • Reinforcement learning is difficult: # 可是强化学习非常困难
    • The rewards are typically delayed so its hard to know where we went wrong (or right). # 反馈通常会延迟
    • A scalar reward does not supply much information. # 并且反馈信息太少
    • 强化学习相比监督/非监督学习，模型参数通常不会太多。强化学习在~1k左右，而监督/非监督在~1m左右。
• Unsupervised learning # 非监督学习
  • Discover a good internal representation of the input. # 从输入中发现内部特征/表示
  • 在近40年里面非监督学习被排除在ML之外，是因为除了来做clustering之外大家都不清楚它能用来做什么。(其实clustering也是一种表示)
  • It provides a compact, low-dimensional representation of the input.
    • High-dimensional inputs typically live on or near a low-dimensional manifold (or several such manifolds).
    • Principal Component Analysis is a widely used linear method for finding a low-dimensional representation.
  • It provides an economical high-dimensional representation of the input in terms of learned features.

types of neural network arch # 神经网络架构类型

• feed-forward neural networks # 前向神经网络
• recurrent neural networks(RNN) # 循环神经网络。适合对序列进行建模（隐藏层可以长时间记忆信息）
• symmetrically connected networks # 对称连接网络(双向对称神经网络)。如果没有隐藏层的话则称为Hopfield nets.

在出现backpropagation算法之前，我们通过随机扰动(pertube)一个或多个weights来训练神经网络(finite difference approximation)，可是实际效果非常差。我们也可以随机扰动隐藏层的激活函数，这样效果会稍好并且效率也更高(因为隐藏层单元数量远小于weights/突触(synapse)数量)。但是依然没有BP好，因为BP可以比较有效地调节所有weights.

BP可以告诉我们dE/dw(error deriviate). 为了得到一个完整的训练神经网络的过程，我们还有两个问题需要考虑：

• Optimization issues: How do we use the error derivatives on individual cases to discover a good set of weights? (lecture 6) # 优化细节
  • How often to update the weights
    • Online: after each training case.
    • Full batch: after a full sweep through the training data.
    • Mini-batch: after a small sample of training cases.
  • How much to update (discussed further in lecture 6)
    • Use a fixed learning rate?
    • Adapt the global learning rate?
    • Adapt the learning rate on each connection separately?
    • Don’t use steepest descent?
• Generalization issues: How do we ensure that the learned weights work well for cases we did not see during training? (lecture 7) # 泛化细节
  • 关于出现overfitting的原因我觉得这里说的特别好
  • The training data contains information about the regularities in the mapping from input to output. But it also contains two types of noise. # overfitting原因是因为数据中会出现噪音
    • The target values may be unreliable (usually only a minor worry). # 结果不一定准确，这个我们没有必要太担心
    • There is sampling error. There will be accidental regularities just because of the particular training cases that were chosen. # 我们需要担心的其实是采样错误。因为采样方式的错误造成我们看到数据呈现的规律，和本身规律不一致。
  • When we fit the model, it cannot tell which regularities are real and which are caused by sampling error. # 如果我们使用有采样错误的数据来做模型训练的话，那么我们没有办法区分，这个规律性是数据本身的，还是因为采样错误造成的
    • So it fits both kinds of regularity.
    • If the model is very flexible it can model the sampling error really well. This is a disaster.
  • 减小sampling error最直接有效的办法就是取更多的数据
  • A large number of different methods have been developed.
    • Weight-decay # 减小weight
    • Weight-sharing # 共享weight, 这样相当于减少自由度
    • Early stopping
    • Model averaging
    • Bayesian fitting of neural nets # 更加复杂的averaging方式
    • Dropout # 随机地关闭隐藏层中的部分单元
    • Generative pre-training

如果最后一层神经元函数是y = e(z) = sigmod(z)，且代价函数是C=(y-t)^2, 那么dC/dz = 2(y-t) * y * (1-y). 如果我们以此来做梯度下降的话会发现：如果t=1,y=0.000001的话，那么dy/dz是非常小的。这样会导致学习速度非常慢，因此我们需要更好的代价函数。我们试图通过将输出转换成为概率，然后使用交叉熵来作为代价函数C = ∑{ti * -log(yi)}(t = 0,1). 为了将输出转换成为概率，我们可以使用softmax function作为神经元函数: yi = e^zi / ∑(e^zj). 这个神经元函数输出不仅仅考虑单个神经突触触发强度，还考虑这层其他神经突触触发强度。使用softmax/cross-entropy之后，dC/dzi = yi - ti. 如果t=1, y = 0.000001的话，那么梯度变化依然会很大。

我们可以使用3-gram(trigram)来做单词预测，通常效果会比较好，但是trigram缺陷是不能够分辨相似的结构。下图是解决这个问题的神经网络模型

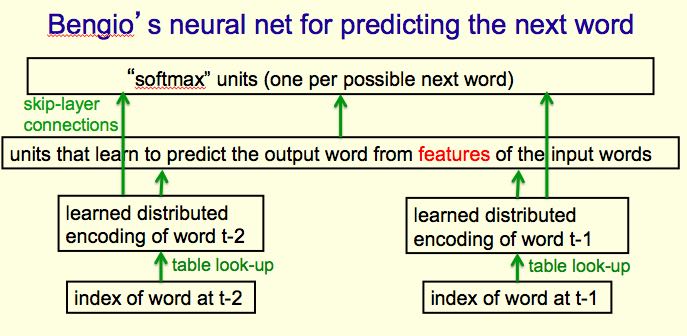
这里稍微说明以下这个模型。假设我们统计出一共有n个词

• "index of word"就是一个大小为n全0的vector, 只有在这个词对应位置上为1.
• "learned distributed encoding"则是单词表示，包含了词性和语义等信息。假设长度为d.
• "units that …"则是预测出来的单词表示。假设长度为k.
• "softmax units"是一个大小为n的vector, 每个位上表示某个词数出现概率。

那么这个神经网络需要训练的参数是2nd + 2dk + kn. 如果n非常大的话(实际也是这样的)那么：k不能太大，除非有足够数据否则容易过拟合；同时k也不能太小，否则我们不能学不到东西。另外对于这么大的输出我们还必须要能正确处理小概率，其实这些小概率的词都是比较重要的。

我们有什么办法来处理比较大规模输出呢？(减小输出集合), 最后面给出了三种方法：

1. 输入word{t-2}, word{t-1}以及candidate, 最后输出logit数值作为选择candidate权重。使用所有的candidates输出的logits再计算softmax，得到每个candidate的概率，然后做cross-entropy作为代价函数。这个方法可以配合n-gram，使用n-gram来做一些candidate的筛选。
2. 将N个词组织成为binary-tree结构(每个tree节点上的向量OR {children}), 然后我们要预测的向量现在变成了v(大小为logN).
3. 输入为word{t-2}..word{t+2}. 但是对于word{t}可以选择输入正确word以及随机word(错误word). 通过增加noise来强化神经网络的训练。

这节介绍了为什么物体识别非常困难，其中一个原因是因为输入图像上平移，旋转，缩放等操作。可是如果这些操作是作用在手写数字图像上的话，那么使用卷积神经网络(convolutional neural network)可以非常好地解决这个问题。CNN大致思想是使用多个不同的feature detectors作用在输入图像上的不同区域，然后我们只需要简单地修改BP算法就可以适应CNN. 如果feature detector1(FD1)输入是9*9的patch的话，那么相当于这个FD1就有81个参数。这个FD1作用在20*20图像上的话，那么可以得到(20-9+1=12) * 12大小的特征向量(#note: 这个特征向量其实就是卷积处理之后生成的图像)。Hinton还给出了两类融入先验知识的方法，其中一类方法是比如修改连通性，修改weight限制，修改激活函数等，另外一类方法是通过先验知识模型模拟出更多的数据这样就可以使用更加复杂模型训练而不会overfitting.

使用mini-batch的时候，我们需要确保每个batch里面的数据分布应该是尽可能典型的。如果数据集合比较大并且冗余度非常高的话，那么使用mini-batch相比full-batch是更加合适的。

mini-batch梯度下降一些技巧

• initial weight.
  1. 如果两个unit的weight(input/output weight)完全一致的话，那么它们学到的feature也是一致的。所以需要在weight增加随机性确保不完全一样。
  2. 如果hidden unit fan-in 比较大的话，那么初始权值最好设置小点，不然会造成拥塞(saturation). 相反如果fan-in比较小的话，那么weight可以设置大一些。可以考虑和1/sqrt(fan-in)成比例。
  3. 和2一样，我们也可以同样这样来scale learning rate. 这样 x * w 就和 1/fan-in成比例了。
• shift input. # 比如(100, 99) -> 0, (101, 100) -> 1的话，我们可以考虑平移100，这样变为(1, -1) -> 0, (1, 0) -> 1. 数据预处理
• scaling input. # 和shift input类似，也是数据预处理。比如(0.1, 100) -> 0, (-0.2, -100) -> 1的话变换成为(1, 1) -> 0, (-2, -1) -> 1.
• decorrelate input. # dimensionality reduction. PCA. 这样可以去除那些两者之间呈线性关系的feature，使得error surface看上去在各个方向上半径一致呈圆球状。

多层网络常见错误：1. 初始learning rate过大，导致一些unit的输出值非常大或者是非常小。但是两种情况都会导致derivative非常小，使得error变化非常小。 2. 过早减小learning rate：过早减小learning rate虽然可能马上有改善，但是之后改善幅度可能会非常小。

下面是几种加速mini-batch学习方法，Hinton对于前三种方法都有比较细的说明： 1. momentum 2. adaptive learning rate 3. rmspop 4. curvature information.

momentum: 假设有个小球在error surface上。梯度下降法是假设小球每次运动完成后都是静止的，所以此次梯度数值直接决定小球运动方向。而momentum方法则是假设小球运动完成后不会停止，所以小球运动方向是上次残留动量和本次动量(梯度数值)的线性组合。ppt 中可以看到对于error surface上有些方向斜长(diagonal ellipses)的问题特别适用，因为每次在这个斜长方向上更新之后，残留冲量会使得每次更新尽可能地沿着斜长(diagonal ellipses)方向。dw = v(t) = a * v(t-1) - x * dE/dw(t). 其中a是冲量系数(或者是粘滞系数viscotiy, 0.5~0.9), x则是learning rate. 初始时候a不要设置太大(0.5), 当梯度变小时在变大a(0.9~0.99). Nesterov改进方法是先进行冲量，然后计算梯度做修正，相当于分开a*v(t-1)和,-x*dE/dw(t)这两项。Hinton的解释是:"it's much better to gamble and then make a correction, than to make correction and then gamble".

seperate adaptive learning rate for each parameter: 不同layer的gradient以及fan-in都不相同，所以为每一层甚至每一个weight搭配一个自适应的learning rate还是会比较有效的。实现上是假设我们有一个global weight(g), 然后每个参数上有一个local gain(x). dw = -dE/dw * g * x. x选择在[0.1,10/100]是比较合适的，初始可以设置为1. adaptive大致思想是：如果两次gradient是同方向的话，那么就增大x = x + k, 否则x = x * (1-k). 比如k=0.05的话，那么x=x+0.05 or x=x*.95. 这种方法比较其实比较适合full-batch, 也可以用于mini-batch, 但是必须确保mini-batch量足够大这样gradient方向变化和whole dataset是一致的。和momentum不同，adaptive learning rate只能处理axis-aligned effects, 而momentum则能处理diagonal ellipses effect, 所以如果两者结合使用的话效果会更好。

rmsprop: 这个方式是rpop的扩展。rpop只能用于full-batch上，并且不考虑gradient magnitude而只考虑gradient sign变化. 这样做的原因是对于那些gradient小的weight可以逃离plateau. learning rate和上面类似但是只涉及乘法：如果两次gradient sign相同，那么x *= k1(1.2), 否则 x *= k2(0.5). 但是最好限制一下上下限[10^-6, 50]. 关于rpop不能用于在mini-batch上，是因为每次mini-batch给出的梯度magnitude可能是不同的：比如我们将full-batch变为10次mini-batch, 前面9次都是相同方向但是梯度magnitude只有0.1, 而第10次变为相反方向但是magnitude有100. stochastic gradient descent主要思想是每次梯度下降都近似于平均值，所以如果直接将rpop作用在mini-batch是不可行的。但是我们可以稍微一些修改，比如我们每次在做mini-batch时候step_size还要除上我们估计的"如果做full-batch对应的梯度magnitude". msq(w,t) = 0.9 * msq(w,t-1) + 0.1 * (dE/dw)^2., mag(w,t) = sqrt(msq(w,t)). 这个公式相当于动态地计算squared gradient的平均值。(#note: 使用方式我觉得是，初始时step_size = 1, last_mag = mag(w,0). 而后step_size *= (k * last_msg) / mag(w,1)).

下面是一张关于神经网络学习方法的总结图：1.什么时候选用full-batch或mini-batch 2. 为什么没有比较简单直接的办法

#note@2015-09-12: 这里有几个关于RNN的文章和视频. 对于理解RNN非常有帮助

• The Unreasonable Effectiveness of Recurrent Neural Networks (视频)
• Understanding LSTM Networks # 据我理解, LSTM是RNN一种实现方式.

RNN实现上可以认为是将其展开成为多层前馈神经网络. 假设我们考虑长度为100的sequences, 那么就可以展开成为100个前馈神经网络. 如果每个前馈神经网络包含N个hidden units的话, 那么RNN就包含100 * N hidden units. 乍看上去weights会比较多, 但是因为weight sharing, 所以可以减少一部分需要训练的weights.

将RNN展开之后, 可以看到这个神经网络层次非常深, 所以使用BP来训练时, 会出现gradient vanish或是explode的问题, 所以其实训练起来非常困难. 下面是4种训练RNN的有效办法:

避免overfitting大致上有下面4中方法，这节只讨论Approach2. 后面一节讨论3,4

• Approach 1: Get more data! Almost always the best bet if you have enough compute power to train on more data.
• Approach 2: Use a model that has the right capacity: 1. enough to fit the true regularities. 2. not enough to also fit spurious regularities (if they are weaker).
• Approach 3: Average many different models. 1. Use models with different forms. 2. Or train the model on different subsets of the training data (this is called “bagging”).
• Approach 4: (Bayesian) Use a single neural network architecture, but average the predictions made by many different weight vectors.

方法2是控制模型所蕴含的假设的容量，也就是控制模型的复杂度，具体有这些方法： 1. architecture(调整神经网络结构比如减少layers和units) 2. early-stopping 3. weight-decay 4. noise.

• early-stopping只所以有效是因为，当weight比较小的时候logistic函数近似线性函数，所以整个神经网络近似线性模型。
• noise本质上效果就是weight-decay：如果我们在输入上加入N(0,e^2)高斯分布噪音的话，那么经过线性组合之后这个噪音就变为N(0, w^2 * e^2)了，那么在cost-function里面就增加了e^2 * w^2这样的惩罚项。如果噪音方差是e^2的话，那么想当增加L2惩罚项，惩罚系数是e^2. 当然noise还可以出现在weight以及activity上.
• weight decay可以有两种方式，一种是weight penalty将weight直接作为惩罚项，另外一种是weight constraint是对weight总体进行约束。虽然weight constraint可以通过拉格朗日乘子转换成为weight penalty形式，但是在实践上weight constraint可以有另外的做法：如果layer上weights超过一定限制的话，我们可以进行放缩操作。反之如果weights过小的话，我们也可以合理地进行放缩操作来避免陷入0附近。我们可以合理地选择penaly函数来控制我们想如何控制weight收敛性。

我们可以从假设极大化后验概率出发来推导出weight-decay. 我们假设output和weight先验都服从高斯分布的话，极大化后验概率其实就是最小化残差+L2惩罚项。观察这个公式我们可以得到一个启示是，对于weight的惩罚系数，我们最好选择(Ed/Ew)^2.

关于mixture of experts这个小节我没有完全理解，大致意思是如果我们需要构造几个模型的话，我们应该：1. 尽可能地让这几个模型可以合作工作（cooperation, 放在一起得到比较好的效果） 2. 但是同时让模型看上去差异比较大(specialization)。

full-bayesian learning不仅要求给出极大后验概率的模型，还要给出所有可能的模型以及对应的后验概率。使用full-bayesian来做预测应该是∑ p(m) * p(y | x, m)并且不会出现overfitting情况(理论上): 出现overfitting是因为我们只是选择某一个模型来作为最终模型，而full-bayesian给出了所有可能的模型和概率。

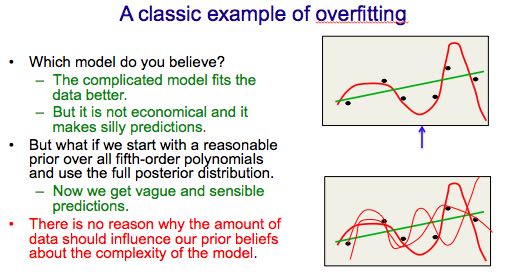
可是在现实情况中我们很难枚举出所有模型同时这些模型非常不太好，所以一个办法是我们可以根据模型(weights)的后验几率，根据这个后验几率在这个weights附近随机选取一些weights，然后将这些weights全部组合起来使用。因为根据原来weight的后验几率来做随机选择，所以也称Markov Chain Monte Carlo(MCMC).

介绍Dropout之前首先要融合两个模型的办法(所以可以认为Dropout是融合多个模型的一种办法)，假设A预测为[0.3,0.2,0.5], B预测为[0.1,0.8,0.1]的话，第一种是mixture则是求解平均值[0.2,0.5,0.3], 第二种是product(sqrt(a * b)然后归一化平均值是[sqrt(0.3 * 0.1), sqrt(0.2 * 0.8), sqrt(0.5 * 0.1)]的归一化。dropout一点比较神奇的地方是，在训练时候如果每次dropout一半的unit的话，然后在预测时对weight取半(*0.5)的话，那么效果相当于是product融合(???, hinton称之为mean-net). Dropout过程是每次训练一个数据的时候将每一层一半的units关闭(做BP的话也不更新对应的weight)，它有非常好的特性体现在：1. 假设有H个units的话，相当于我们从2^H个models里面进行抽样，并且只feed一条训练数据。这是bagging的一种极端情况。 2. 两次训练之间使用的model其实是有weight-sharing的，这就意味着模型同时做了正规化。在实践过程中我们也可以对部分input-unit做dropout, 但是比率应该相对比较低。Hinton谈到关于自己如何想到dropout也挺有意思的：如果我们使用全部的节点来拟合这些数据的话，那么需要依靠所有节点之间非常缜密的配合才能做到。但是依靠所有节点非常缜密的配合这点本身就不可靠，我们更希望部分节点之间就能够比较好地进行工作。

the fog of progress & why we can not predict long-term future