机器学习技法 on Coursera

• 将w0单独剥离出来，wx + w0. 那么w称为coefficient（系数），w0称为bias/intercept(截距)
• svm: learn fattest hyperplanes with help of support vectors. 利用支持向量来找到最胖的超平面
• margin: distance from support vectors to fattest hyperplanes. 间隔就是这些支持向量到超平面的距离
• svm策略函数 min(0.5 * w' * w), st. y(wx + b) >= 1. 二次规划(QP, Quadratic Programming)问题
• svm能够做到比较好的效果，直接上分析有几个：
  • 和regularization公式非常类似
  • 因为hypothesis的分类(dichotomies)更少，所以算法的"vc-dimension"也就越低，也就有更好的泛化能力。
  • 结合non-linear transform, 既能选择出比较好的边界，又能保证复杂度比较低。

• 使用在正则化中使用的Lagrange Multiplier技术，引入L(b,w,a) = 0.5 * w' * w + a * (1 - y(wz + b))，svm策略函数变为min{b,w} (max{a>=0} L(b, w, a)).
• 上面那个策略函数的Lagrange对偶问题（广义拉格朗日函数的极大极小问题）是将min和max调换位置：min{b,w}(max{a>=0} L(b,w,a)) >= max{a>=0}(min{b,w} L(b,w,a)).
• 上面不等式中的=如果满足的话（限制条件），那么称两个问题之间有强对偶关系。如果上面两个函数有强对偶关系的话，那么我们只需要求解后面一个函数即可。
• 将max{a>=0}(min{b,w} L(b,w,a))做推导简化就可以得到a的最优解，这个最优解a和b,w之间的关系称为KKT最优化条件。
• 
• 如果将上面的式子展开并且将max转换称为min的话，就可以看到我们实际上得到了一个N个变量，N+1个约束条件的二次规划问题。
• 
• 下面是SVM的原始形式(Primal)和对偶形式(Dual)的比较。可以看到两个形式在意义和实现上都存在差别。
• 
• 注意Dual形式里面并没有避开高维特征的计算，只不过将高维特征计算隐藏到了高维向量内积计算中。我们可以通过核方法来加速这个部分的计算。

• 高维向量内积部分是zn .* zm = p(xn) .* p(xm). 引入核函数K(xn, xm) = p(xn) .* p(xm). 并且K的计算代价相对更小。
• 
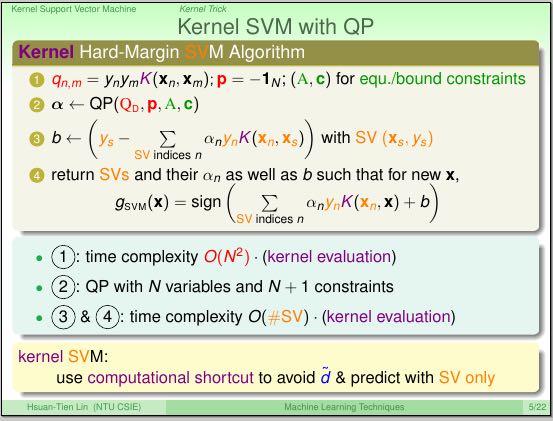
• Polynomial Kernel. 多项式核函数
  • Poly-2. p(x) = scale(sqrt(2*r)在1次多项式，r在2次多项式), 那么K(x,y) = (1 + rxy)^2. 称为K2.
  • Poly-n. Kn = K(x,y) = (b + rxy) ^ n. 其中b控制常数项，n控制多项式项。
  • Poly-1. K1 = K(x,y) = (b + rxy). b和r都不是特别有帮助，所以可以直接设置为0和1. 这也是Linear Kernel.（不过如果是LK的话，那么其实使用Primal形式也可以有效求解）
  • 高维度对于数值计算稳定性是个挑战，另外考虑到过拟合问题，所以维度通常不会选择太高。如果是低维度的话，可能直接映射然后使用linear方式求解可能会更快。
• Gaussian Kernel. 高斯核函数
  • 我们对高斯核函数进行分解，看到高斯核函数其实是无限多维度多项式映射函数。不过这样一来我们也比较难解释w的意义。
• 
• 但是如果我们判定函数来看这个高斯核函数的话，则是以# of SV个以xn为中心的高斯函数的线性组合。也叫做RBF(Radial Basis Function).
• 
• 如果r越大的话，说明方差越小。如果r很大的话：从RBF角度考虑的话，边界就是只是围绕那些SV的高维曲面；从多项式考虑的话，就是用了非常高维的多项式来做你和。最终结果就是泛化能力非常差。

• 因为硬间隔(Hard-Margin)必须要完美地分类数据，所以容易学习到复杂判定函数出现overfitting. 软间隔则放开这个条件允许部分数据错误分类。
• 引入e来放宽限制，但是同时将e加入到极小值部分，我们就得到下面的公式。其中C代表对错误的惩罚：C越大表示我们越不能容忍错误，C越小则表示我们希望容忍错误来达到margin更大。因为我们只是引入了e一次式，所以我们依然可以通过QP来求解。
• 
• 参考Hard-Margin SVM中的推导方法，我们同样可以对上面不等式求解对偶形式，引入核函数。
• 下图是对a物理意义的解释，并且将点进行分类：对于violated的点还可以分为两类，一类是归类正确但是在margin里面，另外一类则是归类错误。
• 
• E{loocv} <= nSV / N. 所以利用nSV可以来估计错误上限。如果做CV比较花时间的话，那么可以参考nSV来做安全检查。如果nSV比较大的话那么就需要小心过拟合。

• 之前线性SVM已经提到和正规化的关系，这里再看看广义SVM和正则化之间的联系，以及各个相式和系数之间的关系。
• 
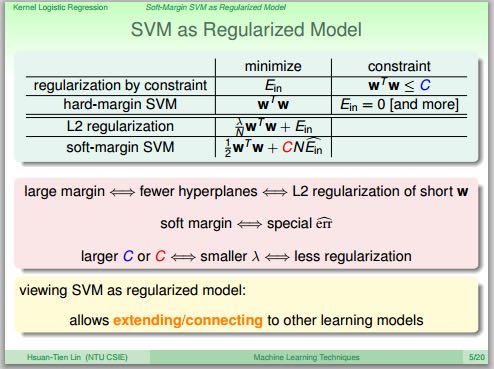
• SVM的损失函数也是err0/1损失函数的上限，但是效果比逻辑回归损失函数要稍微好些。我们可以近似地认为，求解了一个正规化的逻辑回归，相当于求解了一个SVM.
• 概率SVM(Probabilistic SVM): 先求解出w,b 然后将计算出z = w * p(x) + b（可以修改为使用核函数），之后将(z,y)作为逻辑回归训练数据给出概率。但是使用这个办法，我们需要费劲力气求解SVM，然后带入逻辑回归。我们观察，如果w可以表示称为p(x)的线性组合的话，那么在w * p(x)的时候就可以使用核技巧了。
• 有个数学特性是：对于任何L2正规化线性模型，w都可以表示称为b * z线性组合。我们利用这个特性将w带入的话，就可以引入核函数然后使用优化办法如梯度下降来求解。如果带入函数是逻辑回归的话，那么我们就可以得到KLR(Kernel Logistic Regression). 也就是说任何L2正规化线性模型都可以使用核技巧（核函数）。但是相对KLR, 现实中我们使用Probabilistic SVM更多一些。
• 注意上面的b是非常稠密(dense)的，并且在预测时候需要计算b * K(x, x')，时间复杂度是O(N).

• 使用上一节最后说的：“任何L2正规化线性模型都可以使用核技巧”，我们可以同样为ridge regression引入核技巧，叫做Kernel Ridge Regression(LSSVM, Least-Squares SVM)。不过引入核技巧之后在计算效率和灵活性上和原有的线性模型有点差别。
• 
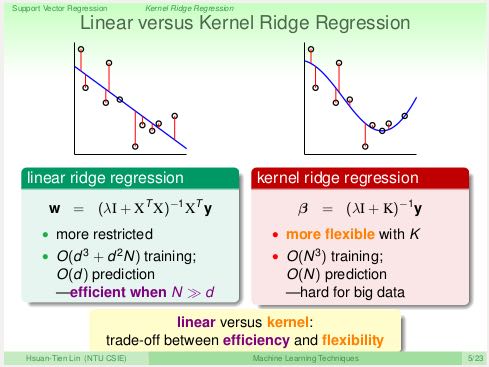
• LSSVM和KLR一样，b也非常稠密，预测时复杂度也是O(N). 并且SVs数量也更多。那么我们是否有办法得到稀疏的b来加快回归预测。
• 
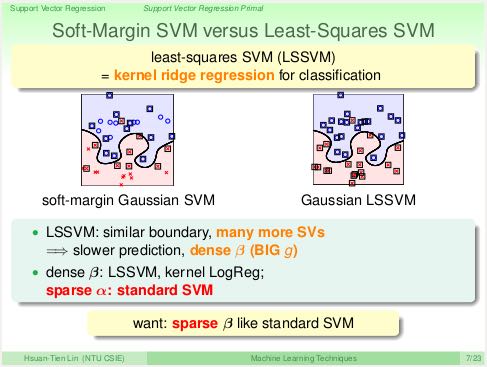
• 上面的问题可以通过引入Tube Regression来解决，这个模型糅合了Ridge Regression和Soft-Margin的特性，来得到最终的SVR. SVR的b相对更加稀疏，SVs数量也更少。

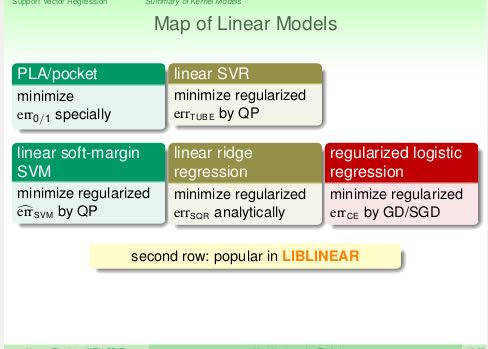
下图是线性模型的总结，包括使用的误差函数以及常用算法。其中linear-SVM(soft-margin), linear-ridge-regression(LRR), regularized LR算法实现在LIBLINEAR里面可以找到。通常来说我们不太可能使用PLA或者是linear-SVR，因为linear-SVM和LRR相对于它们性能更好。

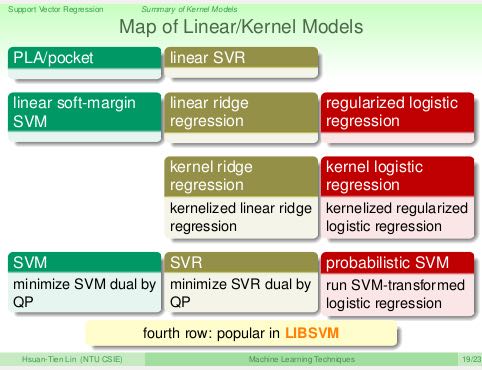
下图是线性模型和核模型的对比总结。其中SVM，SVR，Probabilistic SVM(P-SVM)是算法实现LIBSVM里面可以找到。通常来说我们不太可能使用KRR和KLR，因为SVR和P-SVM相对于它们可以得到更稀疏的空间系数（稳定性，效率以及泛化能力可能都会更好）。

• 我们可以通过聚合(aggregation)方式，也就是混合(blending)各种假设来提高假设准确性。这个和selection有点不太一样：selection是从各种假设中挑选一个假设出来，而aggregation则是将各种假设做组合。
• 可以认为selection是aggregation一种具体方式，除此之外还包括：uniformaly mix(相同的常数权重), non-uniformaly mix(不同的常数权重), conditionally mix(权重是函数)
• 我们可以先从训练数据得到各种hypothesis, blending则可以在CV数据上完成：现将这些h作用在x上得到各种z, 然后利用(z, y)作为输入数据，求解出一个线性(linear-blending)/非线性(any-blending, 也称为stacking)系数。这个线性/非线性稀疏就是各个h的组合系数。注意any-blending方式容易过拟合。
• 
• 为了设计出不同的h, 我们通常会使用下面这几种方法
  • diversity by different models # 不同模型
  • diversity by different parameters # 不同参数
  • diversity by algorithmic randomness # 算法随机性
  • diversity by data randomness # 数据随机性，这个分为两种：一种是随机进行划分训练和CV，另外一种则是从已有数据利用重新抽样的方式生成新的数据集合(bootstrapping).
  • bootstrapping操作是这样的：在大小为N的数据集合上，随机并且可以有放回地取N'次，取出的数据集合大小为N'. bagging是利用bootstrapping重新生成一些新的数据集合，在这些新的数据集合上训练出H，然后将这些h平均组合起来。

• 为每个实例分配权值w进行训练得到假设h0（使用一个相对比较弱的学习算法）。对于错误的点我们加重权值，对于正确的点我们降低权值。然后如果往复得到h1, h2, h3…
• 错误点增加权重，正确点减少权重，这样我们的h0, h1, …才能更加多样，这样组合起来才能够更有优势。这个过程称为re-weighting.
• 假设h的错误率是e, k = sqrt(e/(1-e)), 那么错误点权重w *= k, 正确点权重w /= k. 如果e<=0.5, k>=1，说明假设是有效的所以增加错误点权重。如果e>0.5, k<1, 那么说明这个假设实际上很烂所以需要多学习正确的内容。数学上可以证明这样的re-weighting是optimal的。
• 我们可以使用线性blending方式来组合所有的假设，可以选择线性系数a=ln(k).
• 可以证明上面系数选择是最优的。关于AdaBoost最优化在GBDT这节有分析"Optimization View of AdaBoost"

• Disclaimers about Decision Tree # 决策树的优缺点
  • Usefulness
    • human-explainable: widely used in business/medical data analysis
    • simple: even freshmen can implement one :-)
    • efficient in prediction and training
  • However……
    • heuristic: mostly little theoretical explanations
    • heuristics: ‘heuristics selection’ confusing to beginners
    • arguably no single representative algorithm
  • decision tree: mostly heuristic but useful on its own # 理论上比较难以解释但是却非常实用

• RF通过Bagging方式将多个DT组合在一起。这些DT都是没有经过剪枝，所以有比较大的偏差(variance). 但是这个问题可以通过Bagging来缓解，因为Bagging通过平均可以降低偏差。在学习DT的时候，可以随机选择部分features做decision. 更有甚者可以引入随机矩阵P：这个随机矩阵通过将features空间映射到新的空间，而这个新空间不仅仅是垂直的投影，可以是几个features的线性组合。
• RF在使用Bagging的时候有个附加的好处：就是在生成RF的时候可以同时做validation. 我们分析Out-Of-Bag的几率(经过bootstrapping重新生成数据集合没有取到的记录) = (1-1/N) ^ N ~= 1/e. 可以看到接近1/3的数据记录没有取出，而这个部分的数据我们正好做validation = Eoob. 这里做验证类似于leave-one-out验证：对于每个记录，看有哪些DT没有训练它，然后将这些DT组成RF验证这个记录。最后将所有的记录验证结果取平均。
• RF在做特征选择(feature selection)上也非常有效率。在进行特征选择上一种方法是为某个特征分配随机值，然后观察这个特征随机变化影响性能的程度：如果对性能影响比较小的话，那么就可以剔除这个特征。这种办法称为permutation-test. 因为RF可以在训练时候就完成OOB的验证，而我们可以在验证阶段用DT做预测的时候，从OOB数据集合中选择某个其他记录的feature。
• RF可以给出一个近似平滑的non-linear model，并且如果使用相对多一些树的时候具有比较好的抗噪声的特性。不过RF对于随机性非常敏感，所以在选择树的数目时候，需要确保树的数目能够得到比较稳定的性能。

• AdaBoost算法中我们看到需要为每个实例赋予权值，但是DTree算法中很难处理具有权重的实例。虽然我们可以修改DTree内部算法来处理权重，但是有个相对更简单的办法来处理权重：使用权重来对原来数据集合重新采样或者是重新分布，使得这个权重可以直接反应在数据集合上。这样最后DTree算法只需要处理没有权重的数据集合即可。
• 如果我们使用的是full-grown也就是完全生成树，那么Ein=0. 按照AdaBoost算法，这个k=inf我们没有办法处理。所以DTree内部必须剪枝比如限制树高度，一方面为了具有更好的泛化能力，另一方面为了使得Ein!=0. 另外也可以让DTree只是在某些点上进行训练。如果树高度=1的话，那么AdaBoost-DTree = AdaBoost-Stump.
• Optimization View of AdaBoost:
  • 分析AdaBoost中的权重计算公式，推导之后发现某项和SVM-margin可以关联起来，最终告诉我们需要尽可能地使所有的点权重之和小。搜索最最小值我们可以使用GD方法来完成。
  • 有趣的是我们最终发现，最小值依赖于演算法。只要演算法每一轮给出的h是最优的话，那么最终Eada也是最小的。从另外一个角度来看每轮寻找最优的h本身就是在做梯度下降。
  • GD里面有下降参数a, 通常是固定值. 如果我们每一轮得到h的话，实际上我们可以做一些事情来加快学习速度(称为steepest decent).
  • 如果根据根据正确和错误分类数量来修正a的话，那么a = ln(sqrt((1-e)/e)). 这就解释了为什么AdaBoost这节中通常选择这个值来作为系数。
• GradientBoosting和AdaBoost方法类似，本质上我们都会通过梯度下降学习到h, 然后将这些h线性组合起来作为最终假设，而这个假设数学上可以证明损失函数(近似)最小。和RF不同，两个模型内部每次训练到的小模型，都是具有比较强的泛化能力的。
• 至于两者之间差别，我的理解是，以regression为例，每次迭代中，GradientBoosting是通过拟合残差来得到子模型，而AdaBoost则是根据修改数据点的权重来得到子模型。 两者之间的差别在于，AdaBoost仅仅是GradientBoost的特例(因为GradientBoost允许指定loss function. "For loss ‘exponential’ gradient boosting recovers the AdaBoost algorithm." (scikit-learn)), GradientBoost每次迭代都会根据loss来为本轮生成的小模型指定权重。 这里 有一篇tqchen对于GradientBoost的介绍，see his xgboost.

• 激活函数除了sigmoid之外，还可以是tanh(Hyperbolic Tangent, 双曲正切). tanh(x)=e^x-e^-x / e^x+e^-x. 两者之间还有一些联系tanh(x)=2*sigmoid(2x)-1.
• NN做梯度下降使用backprop算法，总体可以是GD, SGD, 或者是min-batch GD. 在选择初始权重时，应该多选择几组随机值，并且尽可能地小。如果w非常大的话，tanh/sigmoid变化会非常小，容易陷入局部最优。
• NN的dvc = O(VD). 其中V=# of neurons, D=# of weights. 降低dvc有几个办法：1. 使用scaled-L2(weight-elimination) = ∑(w^2/(1+w^2)). 2. Early Stopping.

• Challenges and Key Techniques for Deep Learning
  • difficult structural decisions: # 引入领域知识解决结构问题
    • subjective with domain knowledge: like convolutional NNet for images
  • high model complexity: # 大量数据以及正则化解决复杂模型
    • no big worries if big enough data
    • regularization towards noise-tolerant:
      • dropout (tolerant when network corrupted)
      • denoising (tolerant when input corrupted)
  • hard optimization problem:
    • careful initialization to avoid bad local minimum: called pre-training # 通过预训练选择初始化参数避免局部最优
  • huge computational complexity (worsen with big data): # 计算复杂性通过硬件和分布式解决
    • novel hardware/architecture: like mini-batch with GPU
  • IMHO, careful regularization and initialization are key techniques
• Information-Preserving Encoding/Autoencoder 是三层网络，希望训练出一个identity-function. 因为中间隐藏层将原始信息全部保留，所以也叫做IP-Encoding. 增加正规化项wij(1) = wji(2) = wij.
• Autoencoder对于监督学习可以用来找到信息表示（实际上可以认为是特征选择），也可以做无监督学习(因为y=x)。无监督学习最终可以区分：一种是做identity比较好的数据，另外一种做得不太好。
• 我们可以用Autoencoder来做pre-training, 也就是训练出初始化参数。比如NN是d1-d2-d3-1, 那么d1-d2参数我们可以通过Autoencoder(d1,d2,d1)来求解。
• 前面的Autoencoder是三层网络，隐藏层有非线性变换。如果我们只做线性变换会怎么样呢？这就是linear autoencoder，也可以认为就是PCA. 如果是linear autoencoder的话，其实我们可以通过分析方法来求解这个最优化问题。PCA可以用来做特征选择，这点非常好理解：因为autoencoder在监督学习中就可以找到有效的信息表示。

• RBF Network就是将多个径向函数假设进行线性组合。径向函数(Radial Function)是一种只和中心点距离相关的函数, 所以Gaussian函数是径向函数的一种(Gaussian SVM也是RBF Network的一种).
• 
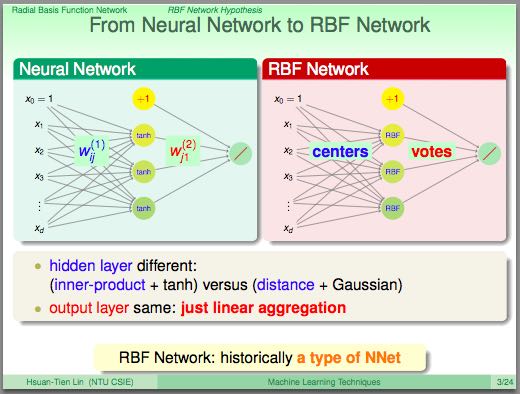
• RBF和Kernel Function都是衡量相似性的函数：RBF是在原始特征空间上的衡量，KernelF则是在非线性变换之后空间上的相似性。
• 我们如何选择这些RBF的中心点呢？Full RBF Network就是以每个实例点作为中心的RBF Network.
• RBF Network可以很容易演化得到kNN. kNN一种办法是使用平均加权，另外一种办法可以通过根据最小二乘来求解线性系数a=(Z'Z)^-1 * Z * y. 其中Z是映射之后的矩阵，并且是方形对称矩阵。
• 如果所有中心点不同的话那么Z还是可逆的，推导一下的话可以得到a=Z^-1 * y. 如果继续化简的话那么g(xi) = yi. Ein(g) = 0. 这种方式成为exact interpolation, 用来做函数逼近(function approximation)。当然这是因为没有增加regularization，如果增加正则化的话那么和ridge regression得到的结果相同。另外一个办法则是选择相对少一些的中心点(也称为prototypes).
• 如何找到这些prototypes? 我们可以把它当做一个clustering问题，K-means是解决这个问题一个非常好的办法。K-means算法是通过alternating minimization(不断交替最小化项)来完成的。

• 回到推荐问题。其实推荐问题也可以表示成为类似AutoEncoder神经网络。因为输入相对比较稀疏，所以我们可以考虑在隐藏层不使用非线性变换，类似使用linear-autoencoder. 说明一下X实际上是n*n的单位矩阵，y就是users-items矩阵。
• 这样最终我们将问题化简成为y = W * V' * X. 其中V是第一层系数矩阵，W是第二层系数矩阵。如果用户数量是n, 推荐物品数量是m, 我们使用隐藏特征数量为d, 那么矩阵大小是V={n*d}, W={m*d}. 因为X是I, 所以y = W * V'. 所以可以看到我们要做的问题其实就变成了矩阵分解。矩阵分解常用于抽取抽象特征。
• 这里的矩阵分解和linear autoencoder给出的矩阵分解不同，下图是两者之间的差别。这里矩阵分解我们只能用交替梯度下降方法来求解V和W。
• 
• 矩阵分解可以使用SGD来做求解，并且SGD似乎是来做大规模矩阵分解最有效的方式。另外作者提到NTU在KDDCup上关于SGD的一个改进：在那次比赛的应用中，越接近现在的实例权重越大。因此他们修改矩阵分解算法，只是使用离现在最近的部分实例来做梯度下降。
•