机器学习基石 on Coursera
https://class.coursera.org/ntumlone-002
- UPDATE@2018-01 在Coursera上面好像拆分成为了两门课程,《机器学习技法》这么课程下架了。
- 在林老师的 主页 上这两门课程的所有材料和视频
L1 机器学习介绍
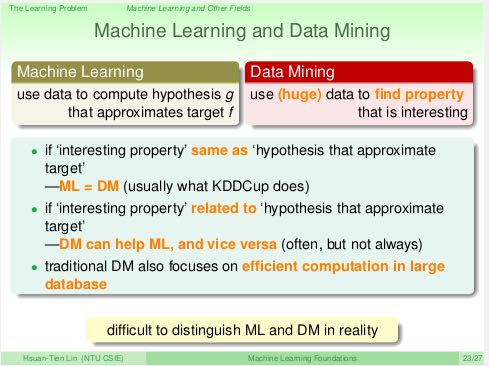
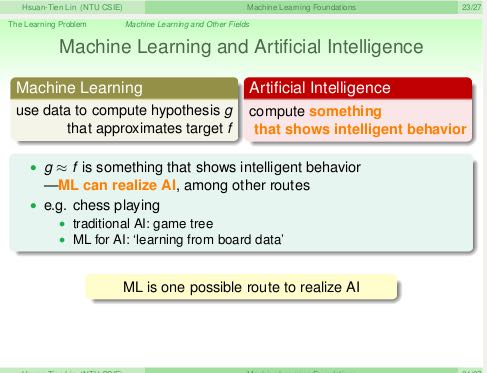
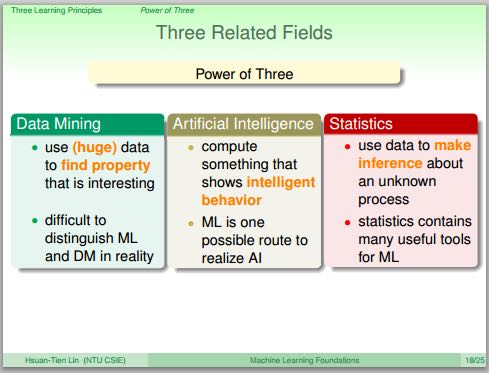
和其他三个领域之间的差别和关系
L2 PLA(Perceptron Learning Algorithm)
L3 机器学习分类
- 输出类型分类:classification/regression/structured(结构化)
- 数据标签分类:supervised/unsupervised/semi-supervised(获得标签代价非常高)/reinforcement(强化,返回反馈满意度)
- 输入方式分类:batch/online/active. 其中online和active都是顺序处理数据,但是active能够主动提问
- 输入特征分类:concrete/raw/abstract. abstract相比raw特征更加隐蔽. 转换为concrete特征需要domain-knowledge来做辅助.
L4-L7 学习可行性分析
- 通常一个模型model会对应很多参数,给定一个参数就对应一个hypothesis. 因此model实际上给出的是一个假设集合hypothesis-set, 我们记为H.
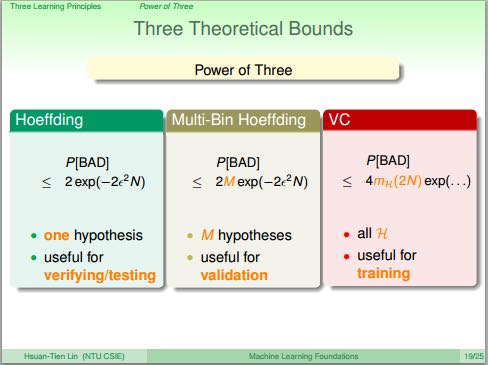
- 从Hoeffding不等式,到H即hypothesis-set的effective-number/break-point,到更加正式的定义vc-dimension.
- vc-dimension只和H有关,或者说只和model有关。vc物理意义是:H处理二分类问题有多少自由度。vc越大说明H选择更多,能力越强,也说明越复杂。
- model/H进行训练效果满足不等式 P(|u-v| > e) <= 2 * (2N)^vc * exp(-2 * e^2 * N). 其中vc是H的vc-dimension.
- 从上面不等式可以看到,vc和N(数据集合大小)之间存在trade-off. vc越大H选择越多,但是需要更多的数据才能找到更好的假设。
L8 噪音和误差
- 引入噪音并不会改变H的vc-dimension. 因此即使训练数据里面包含噪音,我们依然能够进行训练和学习。
- 衡量误差的时候,我们可能会针对false-positive/false-negative给出不同的penalty或者是weight. 这种效果等价于我们对dataset这些错误输入进行virtual-copy.
L9-L11 线性回归,逻辑回归,线性模型
- 线性回归中,使用最小二乘法作为代价函数的话,那么可以使用分析方法计算出w = ((x' * x) ^ -1 * x') * y. 前半部分我们可以称之为pseudo-inverse, 记为x*.
- 线性回归中,如果将w作用在x上的话就可以求解出预测向量y' = x * x* * y = (x * x*) * y. 我们将(x * x*)称为hat-matrix/H.
- 逻辑回归的损失函数,通过合适的缩放,可以看做是err0/1分类损失函数的上限。因此逻辑回归函数可以用来做二分分类。
- OVA(one-versus-all)来求解K多分类问题:1. 需要跑K个二分类问题,每个二分类问题处理N条记录 2. 如果K太大容易造成数据倾斜.
- OVO(one-versus-one)来求解K多分类问题:1. 可以避免OVA出现的数据倾斜问题 2. 需要跑K*(K-1)*0.5个二分类问题,每个二分类问题只处理2*N/K个记录.
L12 非线性变换
L13-L15 过拟合,正则化,验证
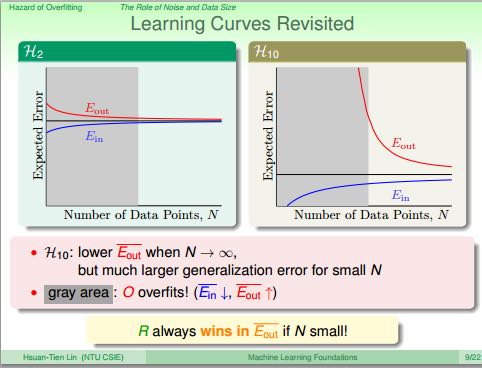
- 泛化能力不好表现loww Ein, high Eout. 过拟合表现是lower Ein, higher Eout.
- 出现过拟合的原因有这些: 1. vc过大 2. 夹杂噪音 3. 数据量不够
- 即使target-function是10th多项式,那么2th多项式H2给出的结果不一定会比10th多项式H10差。虽然可能Ein(H2) > Ein(H2), 但是更有可能是Eout(H2) < Eout(H10).
- 可以看出部分原因我们还没有学习足够多的数据集合
- 而且对于vc越大的H需要学习数据量越大才能获得较好效果
- 噪音可以分为两类:stochastic noise(随机噪音)表示数据集合本身偏差引入的,deterministic noise(确定噪音)表示target-function自身复杂性引入的。
- 比如伪随机数(噪音多)就是使用复杂的(高阶)函数来模拟产生的.
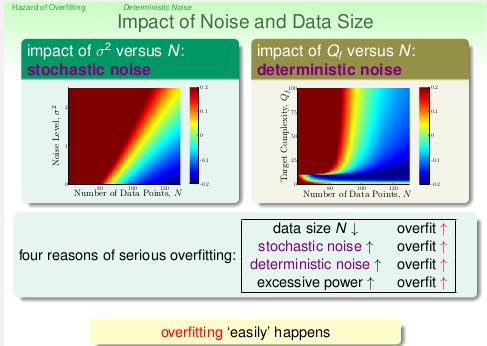
- 解决过拟合问题有下面几个手段 1. 先从简单模型入手 2. data cleaning/pruning 3. data hinting 4.regularization 5. validation
- 引入regularization非常有启发性:通过限制w'w <= C,使用Lagrange Multiplier(拉格朗日乘子法), 推导出weight-decay regularization也就是ridge regression
- 如果需要使用多项式变换的话,应该选用Legendre多项式,可以认为这些多项式之间是相互"正交"的。
- 因为如果我们只是用x^n来做多项式的话,那么高次方的x^n值通常很小,因此要求对应项的w很大。
- 而这与regularization相悖,因为正规化项要求w应该尽可能小。
- 通常使用5~10-Fold来做CV. 训练像是初赛,CV则像是复赛,只有最终测试才是决赛。所以我们要关注应该是测试效果,而不是验证效果。
L16 学习三原则
Sampling Bias(采样偏差)表明我们需要仔细了解数据收集产生的过程。如果收集产生过程本身就有偏差的话,那么我们在训练和验证阶段就需要将偏差考虑进去。
Data Snooping(数据窥视)表明我们不能将测试数据加入训练/CV集合,否则会影响训练效果。机器会学习到这些测试数据的特性,影响到泛化能力。
不要过早地去查看数据来做出假设和模型,但是有时候确实也需要通过观察数据来选择features和模型,因此我们必须在验证的时候严格把关。按照作者的话说应该就是 "careful balance between data-driven modeling(snooping) and validation(no-snooping)."
机器学习和数据挖掘,机器学习和人工智能,机器学习和统计学