10 连抽保底的概率模型

这篇文章是看到云风 云风的 BLOG: 10 连抽保底的概率模型 所想到的。

在云风的文章里面，这个10连抽保底模型最后转换为：

将[0.0, 1.0)之间均匀分布的随机数，转换成为指数分布的随机数，在 这里 可以找到答案：

以指数分布为例，它的CDF(x) = (1 - e ^ (-lam * x)) (x >= 0). 令CDF(x) = p, 那么 x = ln(1-p) / (-lam). ️

然后问题就是如何选择这个lam. 指数分布的期望是E = 1 / lam. 比如lam = 0.1, E = 10，也就是平均需要抽取到10张白卡。 E(也就是lam的选择)直接影响到最终的分布，选择任意的E其实都没有问题（云风在文章里面选择rate=10） 基本上E很大(比如20)的话，那么0-9的分布就更均匀一些，E很小(比如5)的话，那么都会集中在小数字上。 

np.random.seed(42)
def gen(E=9):
    while True:
        p = np.random.random()
        x = int(np.log(1-p) * -E)
        assert x >= 0
        if x < 10:
            break
    return x

Es = [5,9,15,20]
df = pd.DataFrame()
for E in Es:
    xs = pd.Series([gen(E) for i in range(10000)])
    df['E={}'.format(E)] = xs
_ = df.hist(bins = 10, figsize=(20, 10))

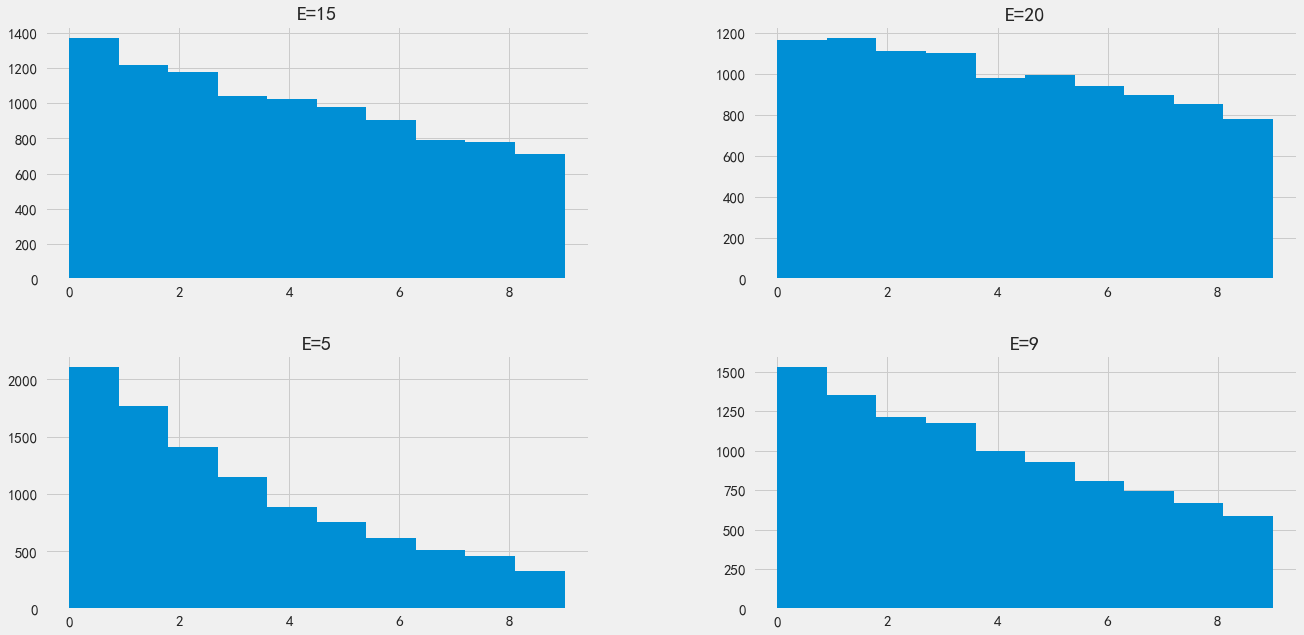
Pasted-Image-20231225104828.png

但是无论如何，最终得到的分布肯定都不再是指数分布了，因为长尾没有了。粗略估计，如果真正要满足指数分布的话，那么应该给予N=9无穷大的概率，E应该是大约在4.5左右才符合指数分布。

让如何让最终分布满足指数分布呢？是否还有更简单的做法呢？ 我觉得可以倒退： 

def est_lam(x, p):
    lam = - np.log(1-p) / x
    return lam

lam = est_lam(9, 0.869) # 这个是多次测试的结果
print('E = {}, lam = {}'.format(1/lam, lam))
v = 0
for i in range(10):
    p = lam * np.exp(-lam * i)
    print('p({}) = {}'.format(i,  p))
    v += p
print(v)


""" Output
E = 4.427918020444273, lam = 0.22583977286455395
p(0) = 0.22583977286455395
p(1) = 0.18018534315870097
p(2) = 0.1437601423230733
p(3) = 0.11469844416006433
p(4) = 0.09151168662016494
p(5) = 0.07301222653361038
p(6) = 0.058252507633495834
p(7) = 0.046476526010727784
p(8) = 0.03708110702488957
p(9) = 0.029585010245256563
1.0004027665745376
"""

数据有这些含义：