CNN(卷积神经网络)入门
http://blog.csdn.net/stdcoutzyx/article/details/41596663 是一篇非常好的关于CNN的入门文章
CNN常用于处理图像和视频数据,在DNN的基础(前向反馈网络结构,使用BP来做参数训练)增加了一些扩展技术: 1. 局部感知(卷积核). 2. 参数共享 3. 多卷积核 4. pooling/subsampling(下采样).
局部感知
卷积神经网络有两种神器可以降低参数数目,第一种神器叫做局部感知野(local receptive fields)。一般认为人对外界的认知是从局部到全局的,而图像的空间联系也是局部的像素联系较为紧密,而距离较远的像素相关性则较弱。因而,每个神经元其实没有必要对全局图像进行感知,只需要对局部进行感知,然后在更高层将局部的信息综合起来就得到了全局的信息。网络部分连通的思想,也是受启发于生物学里面的视觉系统结构。视觉皮层的神经元就是局部接受信息的(即这些神经元只响应某些特定区域的刺激)。如下图所示:左图为全连接,右图为局部连接。
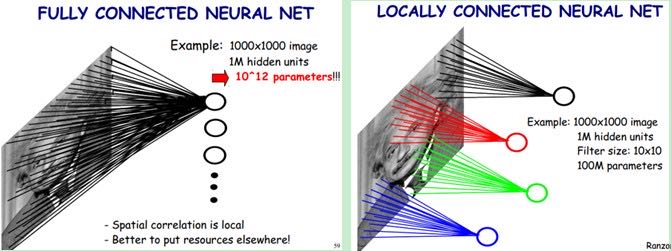
在上右图中,假如每个神经元只和10×10个像素值相连,那么权值数据为1000000×100个参数,减少为原来的万分之一。而那10×10个像素值对应的10×10个参数,其实就相当于卷积操作。
参数共享
但其实这样的话参数仍然过多,那么就启动第二级神器,即权值共享。在上面的局部连接中,每个神经元都对应100个参数,一共1000000个神经元,如果这1000000个神经元的100个参数都是相等的,那么参数数目就变为100了。
怎么理解权值共享呢?我们可以这100个参数(也就是卷积操作)看成是提取特征的方式,该方式与位置无关。这其中隐含的原理则是:图像的一部分的统计特性与其他部分是一样的。这也意味着我们在这一部分学习的特征也能用在另一部分上,所以对于这个图像上的所有位置,我们都能使用同样的学习特征。
更直观一些,当从一个大尺寸图像中随机选取一小块,比如说 8x8 作为样本,并且从这个小块样本中学习到了一些特征,这时我们可以把从这个 8x8 样本中学习到的特征作为探测器,应用到这个图像的任意地方中去。特别是,我们可以用从 8x8 样本中所学习到的特征跟原本的大尺寸图像作卷积,从而对这个大尺寸图像上的任一位置获得一个不同特征的激活值。
如下图所示,展示了一个3×3的卷积核在5×5的图像上做卷积的过程。每个卷积都是一种特征提取方式,就像一个筛子,将图像中符合条件(激活值越大越符合条件)的部分筛选出来。
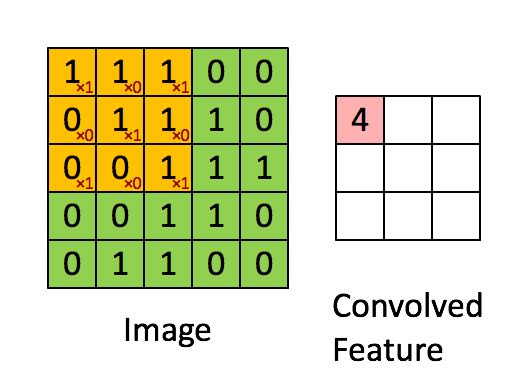
完成前面两个操作之后,假设原始图像大小20 * 20, filter/卷积核大小5 * 5, 那么我们得到卷积之后的图像大小是(20 - 5 + 1) = 16 * 16,每个像素点是有5*5个connections. 所以共有16 * 16 * 5 * 5个connections, 但是只有5 * 5个不同的weights.(因为参数共享原因)
多卷积核
一个filter/卷积核对应这个图像的一种可能特征,实际上我们会想多尝试几种可能的特征,所以我们可以使用多卷积核(或称为feature maps).
上面所述只有100个参数时,表明只有1个10*10的卷积核,显然,特征提取是不充分的,我们可以添加多个卷积核,比如32个卷积核,可以学习32种特征。在有多个卷积核时,如下图所示:
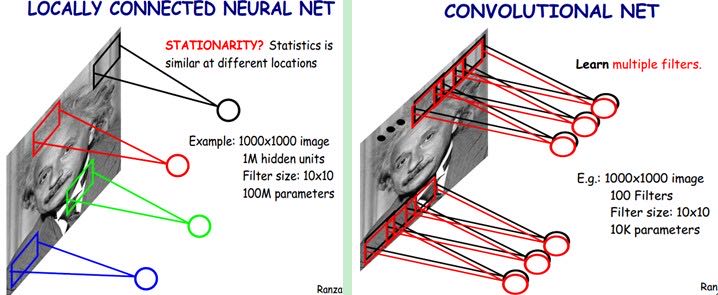
上图右,不同颜色表明不同的卷积核。每个卷积核都会将图像生成为另一幅图像。比如两个卷积核就可以将生成两幅图像,这两幅图像可以看做是一张图像的不同的通道。
还是以上面为例的话,如果我们使用500 feature maps的话,那么我们的connections数目变为16 * 16 * 5 * 5 * 500, 权重数量也变为5 * 5 * 500.
下采样
在通过卷积获得了特征 (features) 之后,下一步我们希望利用这些特征去做分类。理论上讲,人们可以用所有提取得到的特征去训练分类器,例如 softmax 分类器,但这样做面临计算量的挑战。例如:对于一个 96X96 像素的图像,假设我们已经学习得到了400个定义在8X8输入上的特征,每一个特征和图像卷积都会得到一个 (96 − 8 + 1) × (96 − 8 + 1) = 7921 维的卷积特征,由于有 400 个特征,所以每个样例 (example) 都会得到一个 7921 × 400 = 3,168,400 维的卷积特征向量。学习一个拥有超过 3 百万特征输入的分类器十分不便,并且容易出现过拟合 (over-fitting)。
为了解决这个问题,首先回忆一下,我们之所以决定使用卷积后的特征是因为图像具有一种"静态性"的属性,这也就意味着在一个图像区域有用的特征极有可能在另一个区域同样适用。因此,为了描述大的图像,一个很自然的想法就是对不同位置的特征进行聚合统计,例如,人们可以计算图像一个区域上的某个特定特征的平均值 (或最大值)。这些概要统计特征不仅具有低得多的维度 (相比使用所有提取得到的特征),同时还会改善结果(不容易过拟合)。这种聚合的操作就叫做池化 (pooling),有时也称为平均池化或者最大池化 (取决于计算池化的方法)。
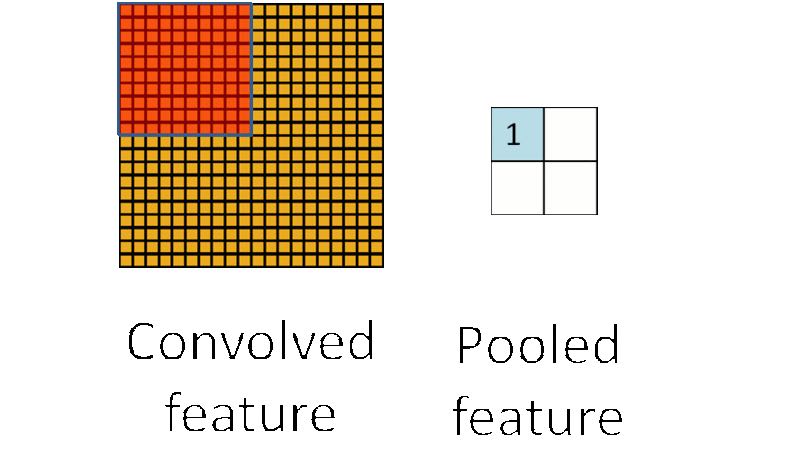
pooling不仅仅能够减少计算量,还可以许多不变性,比如旋转(rotate)不变性,平移(shift)以及扭曲(distortion)不变性。
在实际应用中,往往使用多层卷积,然后再使用全连接层进行训练,多层卷积的目的是一层卷积学到的特征往往是局部的,层数越高,学到的特征就越全局化。下面这幅图就是 LeNet-5 的结构
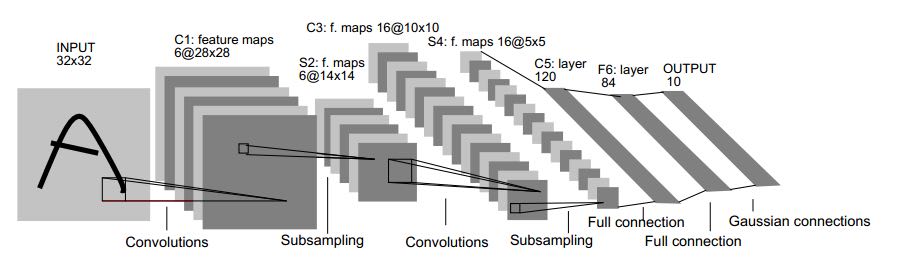
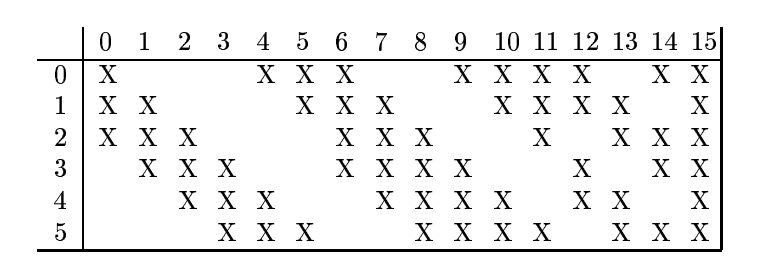
S2有6个fmaps, C3有16个fmaps, 两者之间并不是完全连接的。这样可以打破网络对称性,强迫C3上的不同fmaps根据不同输入学习到互补信息。
As Dr. LeCun explained it, his non-complete connection scheme would force the feature maps to extract different and (hopefully) complementary information, by virtue of the fact that they are provided with different inputs. One way of thinking about this is to imagine that you are forcing information through fewer connections, which should result in the connections becoming more meaningful.
具体连接配置是这样的
另外在关于激活函数方面,这里 的建议是内部使用ReLu, 倒数第二层换成sigmoid, 最后使用softmax. 这里 (还给出了具体实现!)的建议则是使用tanh(作者不太建议使用sigmoid), 最后使用softmax. 不知道能不能综合考虑,内部使用ReLu, 倒数两层换为tanh和softmax.
粗略地看了一下"Gradient-Based Learning Applied to Document Recognition"的Section II.
- 通常图像是具有局部相关性的,所以可以使用local receptive field以及weight sharing.
- 个人理解:使用multiple feature maps可以用来引入旋转(rotate)不变形,可以使用多个卷积核来学习旋转
- pooling可以引入平移(shift)以及扭曲(distortion)不变性
- C5这层实际上是一个卷积层,只不过恰好conv kernel size = 5.
没有太理解F6/Output. 不过在这两层里面值得一体的是,论文里面说如果classes太多的话(比如84种),那么最好不要采用native-bitv方式来定义输出(native-bitv是我随便取的名字,如果classes=84, 那么输出就是84长度的bit-vector,其中有一个bit为1其他全部为0),否则使用sigmoid簇函数作为loss function效果非常差(当然可以使用softmax). LeCun给的方式则是RBF/Euclidean作为loss function, 输出表示方式允许在多个bit上为1. 如果将定义输出表示称为灰度图像的话,就是下面这个样子
