General Algorithm

Table of Contents

1. strlen in glibc

参考链接 http://www.kuqin.com/language/20071113/2308.html. 这里和链接有点不太一样的就是，这个版本glibc实现考虑了非ASCII字符。 

size_t strlen(str)
const char *str;
{
  const char *char_ptr;
  const unsigned long int *longword_ptr;
  unsigned long int longword, himagic, lomagic;

  // 首先是需要对齐到unsigned long int这个长度.
  // 之后就是每个unsigned long int来进行判断.
  // 这样可以加快速度

  /* Handle the first few characters by reading one character at a time.
   * Do this until CHAR_PTR is aligned on a longword boundary.  */
  for (char_ptr = str; ((unsigned long int) char_ptr
                        & (sizeof(longword) - 1)) != 0; ++char_ptr)
    if (*char_ptr == '\0')
      return char_ptr - str;

  /* All these elucidatory comments refer to 4-byte longwords,
   * but the theory applies equally well to 8-byte longwords.  */

  longword_ptr = (unsigned long int *) char_ptr;

  // 为了简化处理的话，我们可以认为sizeof(longword)==8，这样
  // himagic = 0x8080808080808080L
  // lomagic = 0x0101010101010101L

  /* Bits 31, 24, 16, and 8 of this number are zero.  Call these bits
   * the "holes."  Note that there is a hole just to the left of
   * each byte, with an extra at the end:
   *
   * bits:  01111110 11111110 11111110 11111111
   * bytes: AAAAAAAA BBBBBBBB CCCCCCCC DDDDDDDD
   *
   * The 1-bits make sure that carries propagate to the next 0-bit.
   * The 0-bits provide holes for carries to fall into.  */
  himagic = 0x80808080L;
  lomagic = 0x01010101L;
  if (sizeof(longword) > 4) {
    /* 64-bit version of the magic.  */
    /* Do the shift in two steps to avoid a warning if long has 32 bits.  */
    himagic = ((himagic << 16) << 16) | himagic;
    lomagic = ((lomagic << 16) << 16) | lomagic;
  }
  if (sizeof(longword) > 8)
    abort();

  /* Instead of the traditional loop which tests each character,
   * we will test a longword at a time.  The tricky part is testing
   * if *any of the four* bytes in the longword in question are zero.  */
  for (;;) {
    longword = *longword_ptr++;

    // 这里原理非常简单,假设在unsigned long int里面存在一个0的话
    // 那么0-lomagic的话会造成高位为1.如果!=0的话那么至少>=1就不会造成对应字节高字节为1了.
    // 当然这里还有一种情况就是这个不是一个ASCII字符.
    // 使用& ~longword来判断的话,如果高位就为1的话那么就会置为0,这样就排除了非ASCII情况.
    // 然后& himagic的话,来判断是否有高位为1.如果有的话说明这几个字节里面存在0.
    // 如果存在0的话那么就只是针对这8个字节进行枚举

    if (((longword - lomagic) & ~longword & himagic) != 0) {
      /* Which of the bytes was the zero?  If none of them were, it was
       * a misfire; continue the search.  */

      const char *cp = (const char *) (longword_ptr - 1);

      if (cp[0] == 0)
        return cp - str;
      if (cp[1] == 0)
        return cp - str + 1;
      if (cp[2] == 0)
        return cp - str + 2;
      if (cp[3] == 0)
        return cp - str + 3;
      if (sizeof(longword) > 4) {
        if (cp[4] == 0)
          return cp - str + 4;
        if (cp[5] == 0)
          return cp - str + 5;
        if (cp[6] == 0)
          return cp - str + 6;
        if (cp[7] == 0)
          return cp - str + 7;
      }
    }
  }
}

2. consistent hashing

The basic idea behind the consistent hashing algorithm is to hash both objects and caches using the same hash function.The reason to do this is to map the cache to an interval, which will contain a number of object hashes. If the cache is removed then its interval is taken over by a cache with an adjacent interval. All the other caches remain unchanged.

一致性hash基本思想就是将所有对象都使用同样的hash函数进行hash(包括要被分布的对象，以及分布到的位置)。如果某个分布位置被移除的话，那么原本在这个位置上的对象就会分布在临近的分布位置上，而其他的对象却不用移动自己的位置。如果分布位置之间interval间隔过大的话那么可以制作virtual node来使得interval映射足够小，而这些virtual node映射到同一个node节点上面。实际上上述文章中也进行实验证明interval小的话那么standard deviations也变小了，每个node均摊的object基本均匀了：)。

3. rsync core algorithm

首先针对dst文件按照block分别求得checksum和md5.其中checksum用来进行弱校验，md5用来进行强校验。所谓弱校验就是如果checksum不等的话那么文件内容必然不相同，强校验就是如果md5相同的话那么文件内容必然相同。但是checksum还有一个好处，就是可以根据[k,k+n)的checksum,很快地计算出[k+1,k+n+1)的checksum.（非常类似于滑动窗口的工作方式）这点对于在src文件中查找相同块非常重要。将每个块的(checksum,md5)传输到源端。

源端得到每个块的(checksum,md5)之后，根据checksum作为hashcode插入到hashtable中去。这样源端就了解了目的端现在所有块的情况。然后针对src文件做下面操作：

  1. k=0
  2. 读取[k,k+512)字节得到checksum. 注意这个checksum可以很快地计算出来。
  3. 如果这个checksum存在于hashtable中，那么说明这个块可能目的端存在，goto 3. 否则说明肯定不存在目的端，goto 5.
  4. 比较md5是否相同，如果相同的话那么认为block相同，否则不同。
  5. 如果这个checksum不存在于hashtable的话，那么说明肯定不存在目的端，goto 5.
  6. 如果全部处理完毕的话那么退出，否则k+=1.

这里需要注意就是checksum可以很快地类似于滑动窗口的工作方式计算出来.

源端完成了上面这些操作之后，就可以知道那些块目的端是存在的（以及存在于什么地方），自己有那些块是目的端没有的，然后通过传输增量并且文件拼接来达到数据同步的目的。

4. simhash algorithm

simhash算法针对文档分析得到文档特征的一个向量表示，然后使用这个向量之间的差距就可以作为文档之间的差别大小，可以用来做文档近似判断。

simhash算法原理非常简单：

  1. 创建f-bit的V向量初始化为0
  2. 首先针对文档提取一系列特征C{i}（比如可以抽取比较重要的特征词出现次数等），对于每个特征给定一个权重W{i}
  3. 针对每个特征C{i}求出一个f-bit的hash值，遍历hash值每个bit.如果bit=1的话，那么V{i}+=W{i},否则V{i}-=W{i}
  4. 如果V{i}>0那么V{i}=1,否则V{i}=0.这个V{i}就作为这个文档的simhash值

可以看到如果simhash之间的bit相差小的话，那么文档之间的相似度就更高，这里没有证明但是可以比较感性地感觉到。两个simhash之间的bit差异个数叫做海明距离。直接比较两个simhash海明距离非常简单，

现实场景通常是我们已经有一组很大的文档集合S以及对应的simhash值，对于新来的文档d, 哦我们需要判断在S中是否有和d海明距离小于k的文档。

假设S是排好序的个数是N，我们simhash f=64.如果k非常小比如{1,2,3}的话，那么可以枚举和d simhash相差k的所有simhash值，然后再S里面进行检索，时间复杂度在C(64,k)*lgN.但是如果k比较大比如>=10的话，那么我们可以先对S进行分段搜索：

  1. 我们对S进行分段，每次取出2^m个元素，我们确保2^m个元素高位有m’相同。因为S排好序所以通常m'很高。
  2. 我们首先对于m'个位和d simhash高位判断有多少位存在差异，假设x存在差异.这样我们可以在2^m元素判断m-x差异的元素。
  3. 总体思想来说的话就是希望可以缩小搜索集。似乎在算法复杂度上面没有啥改进，可以在实现上改进。

不过话说回来，文档近似判断应该k很小在{1,2}左右, 对应的C(64,k)={64,2016}

UPDATE@201808 这篇 文档 讲的不错，还给出了更好的查询办法，可以预先做好索引加快查询和比对。

我们可以把 64 位的二进制simhash签名均分成4块，每块16位。根据鸽巢原理（也称抽屉原理），如果两个签名的海明距离在 3 以内，它们必有一块完全相同。如下图所示：

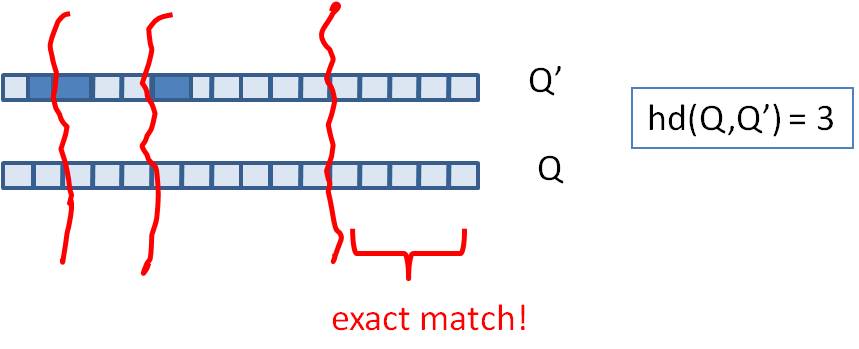
Pasted-Image-20231225105125.png

然后把分成的4 块中的每一个块分别作为前16位来进行查找，建倒排索引。

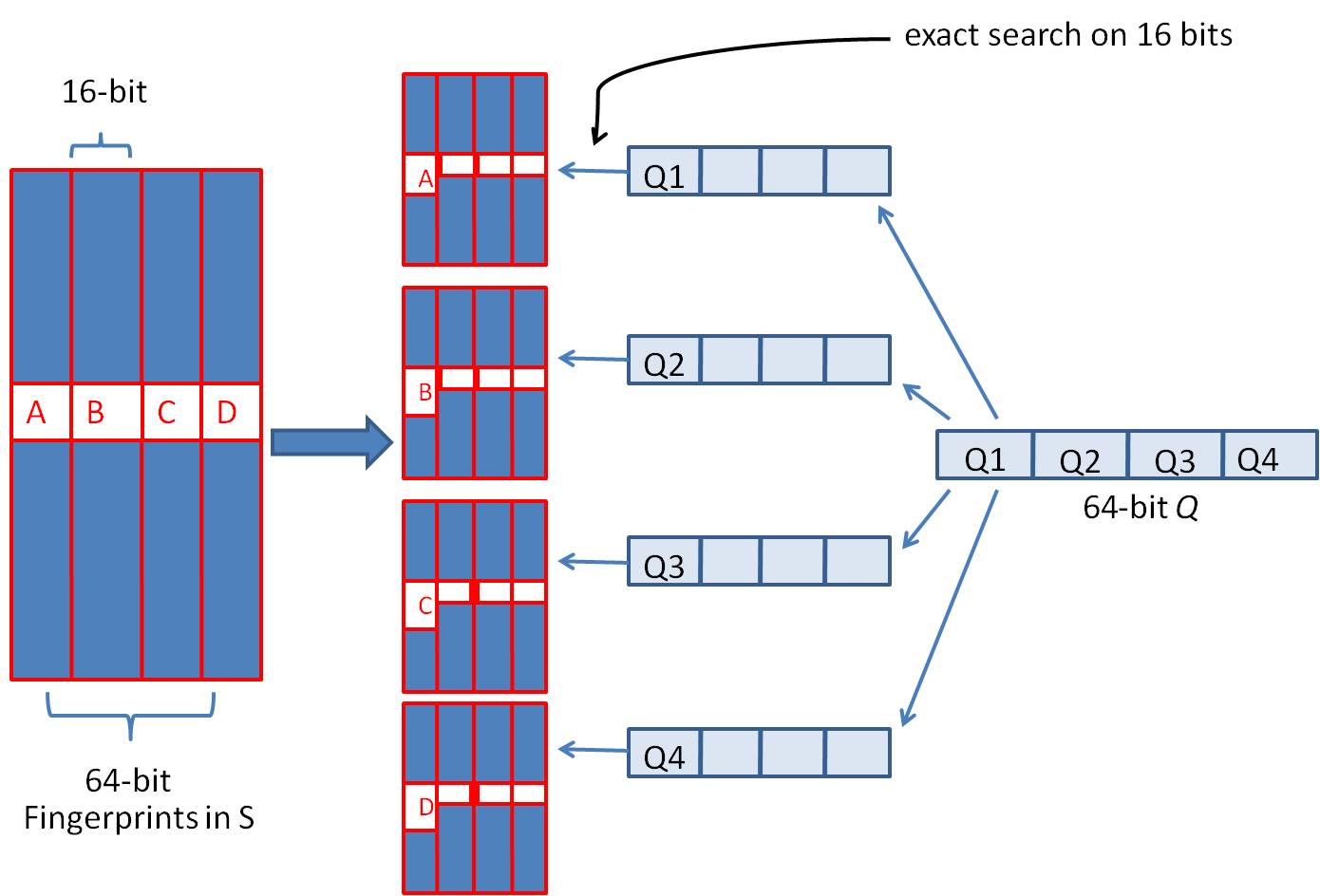
Pasted-Image-20231225105212.png

5. HyperLogLog

这个算法主要是来进行去重的，前提是在big data下面并且内存存在限制。算法的假设和原理如下：

Given a random uniform distribution for likelihoods of N 0s and 1s, you can extract a probability distribution for the likelihood of a specific phenomenon. The phenomenon we care about is the maximum index of a 1 bit. Specifically, we expect the following to be true:

50% of hashed values will look like this: 1xxxxxxx…x 25% of hashed values will look like this: 01xxxxxx…x 12.5% of hashed values will look like this: 001xxxxxxxx…x 6.25% of hashed values will look like this: 0001xxxxxxxx…x

So, naively speaking, we expect that if we were to hash 8 unique things, one of them will start with 001. If we were to hash 4 unique things, we would expect one to start with 01. This expectation can also be inverted: if the “highest” index of a 1 is 2 (we start counting with index 1 as the leftmost bit location), then we probably saw ~4 unique values. If the highest index is 4, we probably saw ~16 unique values. This level of approximation is pretty coarse and it is pretty easy to see that it is only approximate at best, but it is the basic idea behind HyperLogLog.

The adjustment HyperLogLog makes is that it essentially takes the above algorithm and introduces multiple “buckets”. That is, you can take the first k bits of the hashed value and use that as a bucket index, then you keep track of the max(index of 1) for the remaining bits in that bucket. The authors then provide some math for converting the values in all of the buckets back into an approximate cardinality.

Another interesting thing about this algorithm is that it introduces two parameters to adjust the accuracy of the approximation:

  1. Increasing the number of buckets (the k) increases the accuracy of the approximation
  2. Increasing the number of bits of your hash increases the highest possible number you can accurately approximate

下面是这个算法的一个实现： 

def trailing_zeroes(num):
  """Counts the number of trailing 0 bits in num."""
  if num == 0:
    return 32 # Assumes 32 bit integer inputs!
  p = 0
  while (num >> p) & 1 == 0:
    p += 1
  return p

def estimate_cardinality(values, k):
  """Estimates the number of unique elements in the input set values.

  Arguments:
    values: An iterator of hashable elements to estimate the cardinality of.
    k: The number of bits of hash to use as a bucket number; there will be 2**k buckets.
  """
  num_buckets = 2 ** k
  max_zeroes = [0] * num_buckets
  for value in values:
    h = hash(value)
    bucket = h & (num_buckets - 1) # Mask out the k least significant bits as bucket ID
    bucket_hash = h >> k
    max_zeroes[bucket] = max(max_zeroes[bucket], trailing_zeroes(bucket_hash))
  return 2 ** (float(sum(max_zeroes)) / num_buckets) * num_buckets * 0.79402

这个算法上面存在一些差别，就是这个算法实现是假设末尾为0的概率为0.5,末尾为10的概率为0.25，以此类推。最后的0.79402应该是调整系数。

另外还有一个SuperLogLog针对HyperLogLog做了一些改进降低了错误的概率：

  • 去掉30%的最大的bucket，只是计算剩余70%的bucket
  • max_zeroes的计算不是使用geometric mean而是使用harmonic mean

这个算法可以很容易地并行化。可以让每个机器各自维护各自的bucket，最后每个机器上面属于相同的bucket index的bucket进行merge即可。

6. CONCISE

这个算法主要是解决如何压缩一个可组合的整数集合，或者可以是认为如何压缩一个稀疏的bitmap. 链接1主要是介绍了一下背景，在他们的系统里面需要保存一个稀疏bitmap。链接2是原始论文，想了解具体内容还是看看这个比较好。

这个算法应该是在WAH（Word Aligned Hybrid）上改进的。下面是WAH的简单描述

  • WAH是已31bit为一个处理单位，这里我们称为block
  • 如果block里面有0和1的话，那么使用<1> block表示
  • 如果block里面只有0的话，并且连续n个block都是这样的话，那么使用<00> <n>
  • 如果只有1的话，那么前缀使用<01>

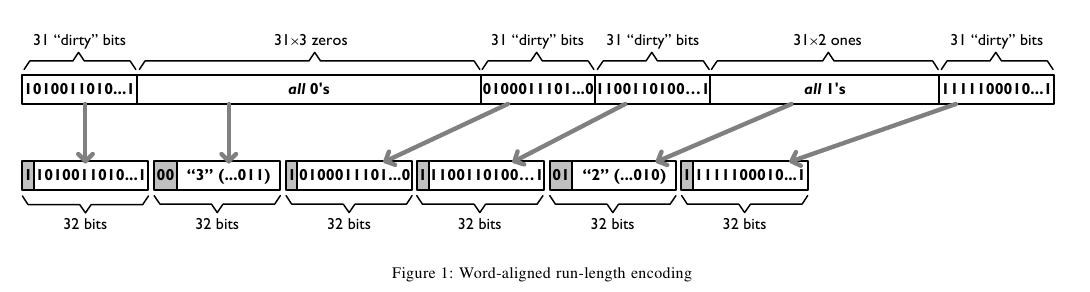
Pasted-Image-20231225103735.png

可以看到其实<n>最长为2^30-1（肯定不会为0）.但是实际上大部分到不了这么长。剩余的空间就会存在浪费。

CONCISE针对这个部分稍微改进了一下

  • the following 5 bits are the position of a “flipped” bit within the first 31-bit block of the fill（剩余的5个bit表示从在第几位存在一个反转，这个可以处理一些特殊情况）
  • and the remaining 25 bits count the number of 31-blocks that compose the fill minus one. (剩余的25个bit表示后面存在多少个31bit blocks)

可以看到最大的范围是31 + 2^25 * 31 = 1040187423 , 如果从0开始的话，那么就是[0,1040187422]

下面是一个例子， Compressed representation of the set {3, 5, 31–93, 1024, 1028, 1 040 187 422}.

  • The word #0 is used to represent integers in the range 0–30,
  • word #1 for integers in 31–92, （5bit为0，说明这个31bit是完全填充。25bit=1表示后面1 * 31个bit全为1，范围就是从31到31(start) + 31 + 31 - 1 = 92.
  • word #2 for integers 93–1022, （5bit为1，说明下一个31bit的第一个元素是反转的也就是93。范围从93到93(start) + 31 + 29 * 31 - 1 = 1022
  • word #3 for integers 1023–1053,
  • word #4 for integers 1054–1 040 187 391,
  • and word #5 for integers 1 040 187 392–1 040 187 422.

Pasted-Image-20231225104457.png

论文后面还给了一些 直接在这种压缩表示 上面的算法。

7. 流式计算均值和方差

需要注意区分如下概念。可以参见wikipedia

对方差计算可以做如下简化, 其中Xi表示第i个元素，Xe表示平均值 

th^2 * n = (X1-Xe)^2 + (X2-Xe)^2 + (X3-Xe)^2 + ... (Xi-Xe)^2 + .. (Xn-Xe)^2
         = (X1^2 + X2^2 + ... Xi^2 + ... + Xn^2) - 2 * Xe * (X1 + X2 + ... Xi + ... Xn) + n * Xe^2
         = (X1^2 + X2^2 + ... Xi^2 + ... + Xn^2) - 2 * Xe * n * Xe + n * Xe^2
         = (X1^2 + X2^2 + ... Xi^2 + ... + Xn^2) - n * Xe^2

8. 查找非重复数字

有一堆数，只有 一个 数出现单次，其余数都出现 偶数 次。

a1 a1 a2 a2 … an an X

这个问题只要将所有的值xor，那么对于a1 xor a1 = 0, 因此结果就剩下X

http://oj.leetcode.com/problems/single-number/ 

class Solution {
 public:
  int singleNumber(int A[], int n) {
    // Note: The Solution object is instantiated only once and is reused by each test case.
    int x = 0;
    for(int i=0;i<n;i++) {
      x ^= A[i];
    }
    return x;
  }
};

有一堆数，只有 两个 数出现单次，其余数都出现 偶数 次。

a1 a1 a2 a2 … an an X Y

这个问题可以简化成为上面一个问题，同样首先将上面所有的值xor, 那么得到m = X xor Y. 然后我们找到m某一个bit为1，假设这个bit为k

然后再次遍历这堆数字，将bit k==1的元素作为一个集合，bit k==0的元素作为一个集合。这样划分的道理是可以确保X，Y肯定分属于两个集合，并且对于每个集合而言，又回到了上面那个问题。

有一堆数，只有 一个 数出现单次，其余数都出现 三次 。

a1 a1 a1 a2 a2 a2 … an an an X

假设每个数字都是64bit的话，我们可以开辟a0(64) a1(64). 然后统计每个数每个bit上面的0，1个数，并且叠加到a0,a1上。a0(i)表示bit i上为0的个数，a1(i)表示bit i上为1的个数。

这样处理之后，遍历a0,a1.如果a0(i) % 3 == 0的话，那么说明a1(i)%3!=0，并且X在bit i上面肯定是为1的，反之亦然。

并且这个处理方法可以扩展到其余数出现 任意次 。

http://oj.leetcode.com/problems/single-number-ii/ 

class Solution {
 public:
  int singleNumber(int A[], int n) {
    // Note: The Solution object is instantiated only once and is reused by each test case.
    int mask[32]; // sizeof(int) == 32;
    memset(mask,0,sizeof(mask));
    for(int i=0;i<n;i++) {
      R(A[i],mask);
    }
    int code = S(mask);
    return code;
  }
  void R(int a,int mask[]) {
    for(int i=0;i<32;i++) {
      if(a & 0x1) {
        mask[i] = (mask[i] + 1) % 3;
      }
      a >>= 1;
    }
  }
  int S(int mask[]) {
    int code = 0;
    for(int i=31;i>=0;i--) {
      code = (code << 1) + mask[i];
    }
    return code;
  }
};

9. Monty Hall Problem

原题是有三扇门，一扇门后面是一辆汽车，后面两扇门没有东西。主持人首先让你选择一扇门，之后主持人打开一扇后面没有任何东西的门，然后主持人问你是否需要更换你的选择？扩展一下这个问题，如果扩展到N(N>=3)扇门的话，那么之前和之后中奖概率分别是多少？

第一步是随机选择那么概率是1/N.但是第二步概率可以这样考虑：

  1. 我当前选择中奖几率是1/N,那么在其他doors后面的几率是N-1/N.
  2. 主持人打开门之后，如果我坚持当前选择的话，中奖几率是没有变化的。剩余的doors后面几率依然是N-1/N.
  3. 而现在剩余的doors只有N-2扇。如果挑选那些剩余doors的话，那么几率是(N-1)/(N*(N-2)).这个几率比1/N要好.

这里如果我们不是换成剩余的doors而是重新选择的话，那么几率依然是(N-1)/(N*(N-1)=1/N.和原来几率是一样的没有变化。

思考的关键在于，主持人这个行为对你当前选择的概率是没有任何影响的。因为无论如何主持人都可以打开一扇空门出来。

UPDATE@2015-09-08: 这个问题是 Monty Hall Problem, 可以通过 模拟 来计算结果

10. 神奇帽子问题 Magical Hat

A bunch of men are on an island. A genie comes down and gathers everyone together and places a magical hat on some people’s heads (i.e., at least one person has a hat). The hat is magical: it can be seen by other people, but not by the wearer of the hat himself. To remove the hat, those (and only those who have a hat) must dunk themselves underwater at exactly midnight. If there are n people and c hats, how long does it take the men to remove the hats? The men cannot tell each other (in any way) that they have a hat.

FOLLOW UP Prove that your solution is correct.

===

This problem seems hard, so let’s simplify it by looking at specific cases.

Case c = 1: Exactly one man is wearing a hat. Assuming all the men are intelligent, the man with the hat should look around and realize that no one else is wearing a hat. Since the genie said that at least one person is wearing a hat, he must conclude that he is wearing a hat. Therefore, he would be able to remove it that night.

Case c = 2: Exactly two men are wearing hats. The two men with hats see one hat, and are unsure whether c = 1 or c = 2. They know, from the previous case, that if c = 1, the hats would be removed on Night #1. Therefore, if the other man still has a hat, he must deduce that c = 2, which means that he has a hat. Both men would then remove the hats on Night #2

Case General: If c = 3, then each man is unsure whether c = 2 or 3. If it were 2, the hats would be removed on Night #2. If they are not, they must deduce that c = 3, and therefore they have a hat. We can follow this logic for c = 4, 5, …

11. 等概率选取链表元素

https://www.geeksforgeeks.org/reservoir-sampling/

等概率选取未知长度的链表中的元素，要求是只能够遍历这个链表一次。下面是代码， 注意这里的wanted会不断地被更新 

int nmatch = 0;
for ( p=list; p!=NULL; p=p->next ){
    if ( rand() % ++nmatch == 0 ){
        wanted = p;
    }
}

这个问题可以如此考虑，假设长度为n，那么最后一个元素被选出（选中）的概率为1/n，然后我们考虑倒数第二个元素选出的概率

  • 倒数第二个元素必须被 选中 ，概率为1/(n-1)
  • 并且确保倒数第一个元素没有被 选中 。因为最后一个选中概率为1/n，所以最后一个元素不被选中概率为(n-1)/n

因此倒数第二个元素被选出的概率为 1/(n-1) * (n-1)/n = 1/n. 同理计算对于每一个元素的概率都是 1/n.

12. CS中最重要的32个算法

http://www.infoq.com/cn/news/2012/08/32-most-important-algorithms

  1. A* 搜索算法
  2. 集束搜索(又名定向搜索，Beam Search)
  3. 二分查找(Binary Search)
  4. 分支界定算法(Branch and Bound)
  5. Buchberger算法
  6. 数据压缩(Data Compression)
  7. Diffie-Hellman密钥交换算法
  8. Dijkstra算法
  9. 离散微分算法(Discrete differentiation)
  10. 动态规划算法(Dynamic Programming)
  11. 欧几里得算法(Euclidean algorithm)
  12. 期望-最大算法(Expectation-maximization algorithm, EM-Training)
  13. 快速傅里叶变换(FFT, Fast Fourier Transform)
  14. 梯度下降(Gradient descent)
  15. 哈希算法(Hashing)
  16. 堆排序(Heaps)
  17. Karatsuba乘法
  18. LLL算法(Lenstra-Lenstra-Lovasz lattice reduction)
  19. 最大流量算法(Maximum flow)
  20. 合并排序(Merge Sort)
  21. 牛顿法(Newton's method)
  22. Q-learning学习算法
  23. 两次筛法(Quadratic Sieve)
  24. RANSAC
  25. RSA
  26. Schonhage-Strassen算法
  27. 单纯型算法(Simplex Algorithm)
  28. 奇异值分解(SVD, Singular Value Decomsition)
  29. 求解线性方程组(Solving a system of linear equations)
  30. Strukturtensor算法
  31. 合并查找算法(Union-find)
  32. 维特比算法(Viterbi)

13. 猜测平均值的2/3

王建硕: 世界不是天才创造的

要求一群人需要在[0,100]之间选择一个数，这个数是大家选择数的平均值的2/3，谁最接近谁就胜出。

这里对大家可能选择的值进行模拟。如果在智商在90一下的话，那么猜测33。每提高3个智商点的话， 他的猜测会在原来的基础上(* 2/3). 我在网上查阅到说智商的方差是15. 

import numpy as np

vs = np.random.normal(loc = 100, scale = 15, size = 100000)

ratio = 2.0 / 3
start = 50

def make_ratio(v):
    x = 90
    res = start
    while v > x:
        x += 3
        res = int(res * ratio)
    return res

guess = [make_ratio(v) for v in vs]

print(sum(guess) * 1.0 / len(guess))

➜  playbook python sim.py
18.11062

不过需要说明但是，(90, 3)这些magic number我都是在知道这个测试结果是[18-20]之间这个事实之后 不断尝试出来的，这个也算是作弊吧。

14. tfidf & bm25

tfidf算法考虑单词在一篇文档出现的次数，和这个单词在所有文档中出现的次数。而bm25算法在tfidf的基础上，将文档的长度包含了进来：如果一篇文章内出现的词数量明显增多的话，那么会对这篇文章进行降权。

下面是tfidf和bm25算法实现，下面实现中tfidf是个变种。 

def tfidf_weight(X):
    """ Weights a Sparse Matrix by TF-IDF Weighted """
    X = coo_matrix(X)

    # calculate IDF
    N = float(X.shape[0])
    idf = log(N) - log1p(bincount(X.col))

    # apply TF-IDF adjustment
    X.data = sqrt(X.data) * idf[X.col]
    return X

def bm25_weight(X, K1=100, B=0.8):
    """ Weighs each row of a sparse matrix X  by BM25 weighting """
    # calculate idf per term (user)
    X = coo_matrix(X)

    N = float(X.shape[0])
    idf = log(N) - log1p(bincount(X.col))

    # calculate length_norm per document (artist)
    row_sums = numpy.ravel(X.sum(axis=1))
    average_length = row_sums.mean()
    length_norm = (1.0 - B) + B * row_sums / average_length

    # weight matrix rows by bm25
    X.data = X.data * (K1 + 1.0) / (K1 * length_norm[X.row] + X.data) * idf[X.col]
    return X

15. 评估simhash

之前了解这个算法，一直没有怎么使用过。最近想到需要做些去重工作，就找个实现来跑跑。 Google 用这个算法来做网页去重工作。

使用的是 https://leons.im/posts/a-python-implementation-of-simhash-algorithm/ 这个python实现，两个类：Simhash是用来计算hash value的，SimhashIndex则是用来计算临近点的。

我没有太关注simhash的实现，在使用上simhash很重要的部分是抽取特征。如何把一段文本抽取出比较好的特征出来，对于计算相似度至关重要。上面文章给的特征实现比较naive 

def get_features(s):
    width = 3
    s = s.lower()
    s = re.sub('[^\w]+', '', s)
    return [s[i:i + width] for i in range(max(len(s) - width + 1, 1))]

相当于把每3个字符当做一个特征，这样的话如果整个text里面很多3字符的内容相似的话，那么就认为相似。宽度越小的话切分出来的特征就更多，计算量就越大。相反如果宽度越大的话，那么就要求整个更多的更宽字符串相似才认为相似，计算量就更小，召回率会下降但是准确度会更高。

对于多语言来来说，抽取特征是个很重要，同时也是很困难的问题。有个小的想法是，是否可以在build index的时候选择加上语言信息，比如3字符串切分出来的话就是”zh:” + 3字符串这样的，然后在查找的时候也使用多种语言去匹配。

simhash是一个计算密集型的算法，而且blog给出的实现就是单文件，所以结合之前的经验可以很容易地用 `cython` 来优化。 `cp simhash.py _simhash.pyx` 然后运行下面程序 `python build_simhash.py build_ext –inplace` 就可以得到 `_simhash.so` 这个文件。 

#!/usr/bin/env python
# coding:utf-8
# Copyright (C) dirlt

from distutils.core import setup
from Cython.Build import cythonize
setup(
    ext_modules=cythonize("_simhash.pyx"),
)

简单地对比了一下性能，运行10000个text, 原始版本的是3.2s, cython优化过的是2.5s, 没有修改任何代码就获得的了20%的性能提升：)