Find LCA using RMQ

https://www.geeksforgeeks.org/find-lca-in-binary-tree-using-rmq/

LCA可以使用 Tarjan 的离线 算法，也可以将这个问题转变成为RMQ. 这个过程并不复杂，但是还比较有启发性。

以下图为例说明这个过程，假设我们需要找到4和9的LCA(2).

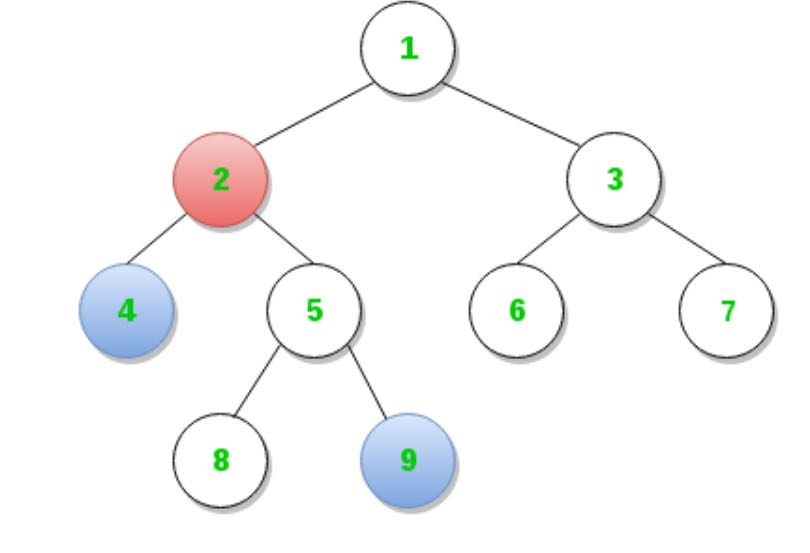
Pasted-Image-20231225104042.png

首先对这个图进行欧拉遍历(Euler Tour)：以类似preorder的方式进行DFS，在进出的时候都记录一次。 不仅记录节点(euler_tour_array)，还记录这个节点所在的depth(depth_array). 得到的结果如下图：

Pasted-Image-20231225103304.png

将euler_tour_array转换成为first_occ_array: 就是每个节点出现在euler_tour_array的第一个下标。 比如4出现第一次出现在euler_tour_array的2号位置，9出现在7号位置。

Observation: The LCA of nodes 4 and 9 is node 2, which happens to be the node closest to the root amongst all those encountered between the visits of 4 and 9 during a DFS of T. This observation is the key to the reduction. Let’s rephrase: Our node is the node at the smallest level and the only node at that level amongst all the nodes that occur between consecutive occurrences (any) of u and v in the Euler tour of T.

We require three arrays for implementation:

  1. Nodes visited in order of Euler tour of T
  2. Level of each node visited in Euler tour of T
  3. Index of the first occurrence of a node in Euler tour of T (since any occurrence would be good, let’s track the first one)

Pasted-Image-20231225104201.png

然后我们需要找到的是在depth_array[2..7]之间，最小的depth的下标。在上面的例子中, 最小的depth是1，对应的是节点2. 正是在这一步需要使用到RMQ. 也就是说，对于交互式LCA查询的话，可以在O(1)时间内转变成为RMQ问题，而RMQ的查询时间是O(lgn).

Algorithm:

  1. Do a Euler tour on the tree, and fill the euler, level and first occurrence arrays.
  2. Using the first occurrence array, get the indices corresponding to the two nodes which will be the corners of the range in the level array that is fed to the RMQ algorithm for the minimum value.
  3. Once the algorithm return the index of the minimum level in the range, we use it to determine the LCA using Euler tour array.