3Blue1Brown
Table of Contents
- 1. Why pi?
- 1.1. Why is pi here? And why is it squared? A geometric answer to the Basel problem
- 1.2. Pi hiding in prime regularities
- 1.3. The most unexpected answer to a counting puzzle
- 1.4. Why do colliding blocks compute pi?
- 1.5. How colliding blocks act like a beam of light…to compute pi.
- 1.6. How pi was almost 6.283185…
- 1.7. The Wallis product for pi, proved geometrically
- 2. Geometry
- 2.1. But why is a sphere's surface area four times its shadow?
- 2.2. The hardest problem on the hardest test
- 2.3. Who cares about topology? (Inscribed rectangle problem)
- 2.4. Ever wondered why slicing a cone gives an ellipse? It’s wonderfully clever!
- 2.5. Sneaky Topology | The Borsuk-Ulam theorem and stolen necklaces
- 2.6. Thinking outside the 10-dimensional box
- 2.7. Circle Division Solution
- 3. Differential equations
- 4. The block collision puzzle
- 5. Physics
- 6. Neat proofs/perspectives
- 6.1. The hardest problem on the hardest test
- 6.2. Why is pi here? And why is it squared? A geometric answer to the Basel problem
- 6.3. Who cares about topology? (Inscribed rectangle problem)
- 6.4. Euler's formula with introductory group theory
- 6.5. All possible pythagorean triples, visualized
- 6.6. But why is a sphere's surface area four times its shadow?
- 6.7. What they won't teach you in calculus
- 6.8. Sneaky Topology | The Borsuk-Ulam theorem and stolen necklaces
- 6.9. Pi hiding in prime regularities
- 6.10. Thinking outside the 10-dimensional box
- 6.11. Ever wondered why slicing a cone gives an ellipse? It’s wonderfully clever!
- 6.12. The Brachistochrone, with Steven Strogatz
- 6.13. Binary, Hanoi and Sierpinski, part 1
- 6.14. Binary, Hanoi, and Sierpinski, part 2
- 6.15. Music And Measure Theory
- 6.16. Circle Division Solution
- 6.17. Euler's Formula and Graph Duality
- 7. Explainers
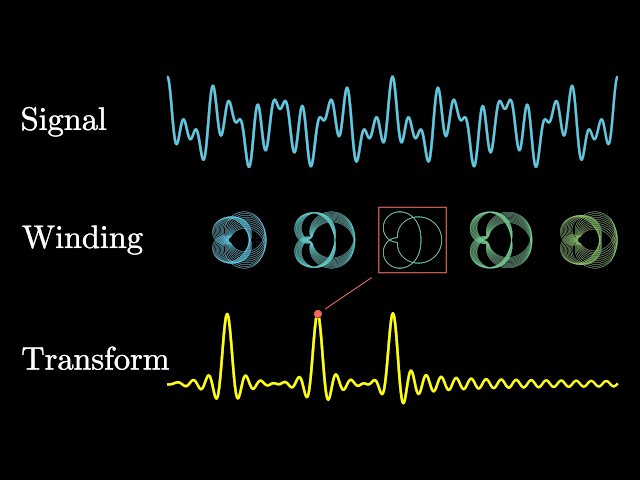
- 7.1. But what is the Fourier Transform? A visual introduction.
- 7.2. But what is a Neural Network? | Deep learning, chapter 1
- 7.3. The Essence of Calculus, Chapter 1
- 7.4. Vectors, what even are they? | Essence of linear algebra, chapter 1
- 7.5. Visualizing the Riemann hypothesis and analytic continuation
- 7.6. But how does bitcoin actually work?
- 7.7. Some light quantum mechanics (with minutephysics)
- 7.8. But what is a Fourier series? From heat flow to circle drawings | DE4
- 7.9. Divergence and curl: The language of Maxwell's equations, fluid flow, and more
- 7.10. Differential equations, studying the unsolvable | DE1
- 7.11. Fractals are typically not self-similar
- 7.12. Visualizing quaternions (4d numbers) with stereographic projection
- 7.13. The more general uncertainty principle, beyond quantum
- 7.14. Hilbert's Curve: Is infinite math useful?
- 8. Neural networks
- 9. Essence of calculus
- 9.1. The Essence of Calculus, Chapter 1
- 9.2. The paradox of the derivative | Essence of calculus, chapter 2
- 9.3. Derivative formulas through geometry | Essence of calculus, chapter 3
- 9.4. Visualizing the chain rule and product rule | Essence of calculus, chapter 4
- 9.5. What's so special about Euler's number e? | Essence of calculus, chapter 5
- 9.6. Implicit differentiation, what's going on here? | Essence of calculus, chapter 6
- 9.7. Limits, L'Hopital's rule, and epsilon delta definitions | Essence of calculus, chapter 7
- 9.8. Integration and the fundamental theorem of calculus | Essence of calculus, chapter 8
- 9.9. What does area have to do with slope? | Essence of calculus, chapter 9
- 9.10. Higher order derivatives | Essence of calculus, chapter 10
- 9.11. Taylor series | Essence of calculus, chapter 11
- 9.12. What they won't teach you in calculus
- 10. Binary, Hanoi and Sierpinski
- 11. Essence of linear algebra
- 11.1. Vectors, what even are they? | Essence of linear algebra, chapter 1
- 11.2. Linear combinations, span, and basis vectors | Essence of linear algebra, chapter 2
- 11.3. Linear transformations and matrices | Essence of linear algebra, chapter 3
- 11.4. Matrix multiplication as composition | Essence of linear algebra, chapter 4
- 11.5. Three-dimensional linear transformations | Essence of linear algebra, chapter 5
- 11.6. The determinant | Essence of linear algebra, chapter 6
- 11.7. Inverse matrices, column space and null space | Essence of linear algebra, chapter 7
- 11.8. Nonsquare matrices as transformations between dimensions | Essence of linear algebra, chapter 8
- 11.9. Dot products and duality | Essence of linear algebra, chapter 9
- 11.10. Cross products | Essence of linear algebra, Chapter 10
- 11.11. Cross products in the light of linear transformations | Essence of linear algebra chapter 11
- 11.12. Cramer's rule, explained geometrically | Essence of linear algebra, chapter 12
- 11.13. Change of basis | Essence of linear algebra, chapter 13
- 11.14. Eigenvectors and eigenvalues | Essence of linear algebra, chapter 14
- 11.15. Abstract vector spaces | Essence of linear algebra, chapter 15
- 12. Shorter videos
- 13. Recommended
- 13.1. Visualizing the Riemann hypothesis and analytic continuation
- 13.2. Who cares about topology? (Inscribed rectangle problem)
- 13.3. Fractals are typically not self-similar
- 13.4. Euler's formula with introductory group theory
- 13.5. All possible pythagorean triples, visualized
- 13.6. Pi hiding in prime regularities
- 13.7. Hilbert's Curve: Is infinite math useful?
- 13.8. What does it feel like to invent math?
- 13.9. But how does bitcoin actually work?
- 13.10. Thinking outside the 10-dimensional box
- 13.11. Some light quantum mechanics (with minutephysics)
- 13.12. The Brachistochrone, with Steven Strogatz
- 13.13. Binary, Hanoi and Sierpinski, part 1
- 13.14. Binary, Hanoi, and Sierpinski, part 2
- 13.15. Music And Measure Theory
- 13.16. Circle Division Solution
- 13.17. Euler's Formula and Graph Duality
- 14. Brachistochrone
- 15. Space filling curves
- 16. Moser Circle Problem
https://www.youtube.com/channel/UCYO_jab_esuFRV4b17AJtAw/playlists
1 Why pi?
1.1 Why is pi here? And why is it squared? A geometric answer to the Basel problem
A most beautiful proof of the Basel problem, using light.Home page: https://www.3blue1brown.com/Brought to you by you: http://3b1b.co/basel-thanksAnd by Brilliant: https://brilliant.org/3b1bBrilliant's principles list that I referenced:https://brilliant.org/principles/Get early access and more through Patreon:https://www.patreon.com/3blue1brownThe content here was based on a paper by Johan Wästlundhttp://www.math.chalmers.se/~wastlund/Cosmic.pdfCheck out Mathologer's video on the many cousins of the Pythagorean theorem:https://youtu.be/p-0SOWbzUYIOn the topic of Mathologer, he also has a nice video about the Basel problem:https://youtu.be/yPl64xi_ZZAA simple Geogebra to play around with the Inverse Pythagorean Theorem argument shown here.https://ggbm.at/yPExUf7bSome of you may be concerned about the final step here where we said the circle approaches a line. What about all the lighthouses on the far end? Well, a more careful calculation will show that the contributions from those lights become more negligible. In fact, the contributions from almost all lights become negligible. For the ambitious among you, see this paper for full details.If you want to contribute translated subtitles or to help review those that have already been made by others and need approval, you can click the gear icon in the video and go to subtitles/cc, then "add subtitles/cc". I really appreciate those who do this, as it helps make the lessons accessible to more people.Music by Vincent Rubinetti: https://vincerubinetti.bandcamp.com/album/the-music-of-3blue1brown------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted on new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: http://3b1b.co/recommendedVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3Blue1BrownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3Blue1Brown
1.2 Pi hiding in prime regularities
A story of pi, primes, complex numbers, and how number theory braids them together.Brought to you by you: http://3b1b.co/leibniz-thanksHome page: https://www.3blue1brown.com/And by Remix: https://www.remix.com/The fact that only primes that are one above a multiple of four can be expressed as the sum of two squares is known as "Fermat's theorem on sums of two squares": https://goo.gl/EdhaN2Music by Vince Rubinetti:https://vincerubinetti.bandcamp.com/album/the-music-of-3blue1brown------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted about new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: http://3b1b.co/recommendedVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3Blue1BrownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3Blue1Brown
1.3 The most unexpected answer to a counting puzzle
If this doesn't blow your mind, I don't know what will.Part 2: https://youtu.be/jsYwFizhncEPart 3: https://youtu.be/brU5yLm9DZMBrought to you by you: http://3b1b.co/clacks-thanksNew to this channel? It's all about teaching math visually. Take a look and see if there's anything you'd like to learn.NY Times blog post about this problem:https://wordplay.blogs.nytimes.com/2014/03/10/pi/The original paper by Gregory Galperin:https://www.maths.tcd.ie/~lebed/Galperin.%20Playing%20pool%20with%20pi.pdfEvidently, Numberphile also described this problem (I had not known):https://youtu.be/abv4Fz7oNr0You'll notice that video has an added factor of 16 throughout, which is not here. That's because they're only counting the collisions between blocks (well, balls in their case), and they're only counting to the point where the big block starts moving the other way.------------------These animations are largely made using manim, a scrappy open source python library: https://github.com/3b1b/manimIf you want to check it out, I feel compelled to warn you that it's not the most well-documented tool, and it has many other quirks you might expect in a library someone wrote with only their own use in mind.Music by Vincent Rubinetti.Download the music on Bandcamp:https://vincerubinetti.bandcamp.com/album/the-music-of-3blue1brownStream the music on Spotify:https://open.spotify.com/album/1dVyjwS8FBqXhRunaG5W5uIf you want to contribute translated subtitles or to help review those that have already been made by others and need approval, you can click the gear icon in the video and go to subtitles/cc, then "add subtitles/cc". I really appreciate those who do this, as it helps make the lessons accessible to more people.------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted on new videos, subscribe: http://3b1b.co/subscribeVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3blue1brownReddit: https://www.reddit.com/r/3blue1brownInstagram: https://www.instagram.com/3blue1brown_animations/Patreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brown
1.4 Why do colliding blocks compute pi?
Part 1: https://youtu.be/HEfHFsfGXjsPart 3: https://youtu.be/brU5yLm9DZMHome page: https://www.3blue1brown.comBrought to you by you: http://3b1b.co/clacks-thanks Many of you shared solutions, attempts, and simulations with me this last week. I loved it! Y'all are the best. Here are just two of my favorites.By a channel STEM cell: https://youtu.be/ils7GZqp_iEBy Doga Kurkcuoglu: http://bilimneguzellan.net/bouncing-cubes-and-%CF%80-3blue1brown/And here's a lovely interactive built by GitHub user prajwalsouza after watching this video: https://prajwalsouza.github.io/Experiments/Colliding-Blocks.htmlNY Times blog post about this problem:https://wordplay.blogs.nytimes.com/2014/03/10/pi/The original paper by Gregory Galperin:https://www.maths.tcd.ie/~lebed/Galperin.%20Playing%20pool%20with%20pi.pdfFor anyone curious about if the tan(x) ≈ x approximation, being off by only a cubic error term, is actually close enough not to affect the final count, take a look at sections 9 and 10 of Galperin's paper. In short, it could break if there were some point where among the first 2N digits of pi, the last N of them were all 9's. This seems exceedingly unlikely, but it quite hard to disprove.Although I found the approach shown in this video independently, after the fact I found that Gary Antonick, who wrote the Numberplay blog referenced above, was the first to solve it this way. In some ways, I think this is the most natural approach one might take given the problem statement, as corroborated by the fact that many solutions people sent my way in this last week had this flavor. The Galperin solution you will see in the next video, though, involves a wonderfully creative perspective.If you want to contribute translated subtitles or to help review those that have already been made by others and need approval, you can click the gear icon in the video and go to subtitles/cc, then "add subtitles/cc". I really appreciate those who do this, as it helps make the lessons accessible to more people.Music by Vincent Rubinetti.Download the music on Bandcamp:https://vincerubinetti.bandcamp.com/album/the-music-of-3blue1brownStream the music on Spotify:https://open.spotify.com/album/1dVyjwS8FBqXhRunaG5W5u------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted on new videos, subscribe: http://3b1b.co/subscribeVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3blue1brownReddit: https://www.reddit.com/r/3blue1brownInstagram: https://www.instagram.com/3blue1brown_animations/Patreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brown
1.5 How colliding blocks act like a beam of light…to compute pi.
The third and final part of the block collision sequence.Part 1: https://youtu.be/HEfHFsfGXjsPart 2: https://youtu.be/jsYwFizhncEHome page: https://www.3blue1brown.comBrought to you by you: http://3b1b.co/clacks-thanksError correction: I wrote the answer as floor(pi/theta), when really it should be ceiling(pi/theta) - 1 t account for values of theta perfectly dividing pi. For example, the case of equal masses gives an angle of pi/4, and 3 total clacks.This beautiful result, and the solution shown here, are due to Gregory Galperin:https://www.maths.tcd.ie/~lebed/Galperin.%20Playing%20pool%20with%20pi.pdfAnd here's a lovely interactive built by GitHub user prajwalsouza after watching this video: https://prajwalsouza.github.io/Experiments/Colliding-Blocks.htmlSpeaking of looking glass universes...https://www.youtube.com/user/LookingGlassUniverseNY Times blog post about this problem:https://wordplay.blogs.nytimes.com/2014/03/10/pi/The plushie pi shown at the video's start:https://www.3blue1brown.com/storeIf you want to contribute translated subtitles or to help review those that have already been made by others and need approval, you can click the gear icon in the video and go to subtitles/cc, then "add subtitles/cc". I really appreciate those who do this, as it helps make the lessons accessible to more people.Music by Vincent Rubinetti.Download the music on Bandcamp:https://vincerubinetti.bandcamp.com/album/the-music-of-3blue1brownStream the music on Spotify:https://open.spotify.com/album/1dVyjwS8FBqXhRunaG5W5u------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted on new videos, subscribe: http://3b1b.co/subscribeVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3blue1brownReddit: https://www.reddit.com/r/3blue1brownInstagram: https://www.instagram.com/3blue1brown_animations/Patreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brown
1.6 How pi was almost 6.283185…
Happy pi day! Did you know that in some of his notes, Euler used the symbol pi to represent 6.28..., before the more familiar 3.14... took off as a standard?Home page: https://www.3blue1brown.comPlushie creatures now available: http://3b1b.co/storeThe idea for this video, as well as the live shots, came from Ben Hambrecht, with the writing and animating done by Grant Sanderson. Special thanks to: - University Library Basel, for letting us rummage through their historical collection - Martin Mattmüller from the Bernoulli-Euler center for helpful discussion - Michael Hartl, author of the Tau Manifesto, for pointing us to obscure references - Library of the Institut de FranceCinematographer: Eugen HellerMusic by Vincent Rubinetti: https://vincerubinetti.bandcamp.com/album/the-music-of-3blue1brown------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted on new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: http://3b1b.co/recommendedVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3Blue1BrownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3Blue1Brown
1.7 The Wallis product for pi, proved geometrically
A new and more circularly proof of a famous Wallis product for pi.Here's a supplemental blog post, expanding some of the rigor of this proofs, along with other interesting tidbits about surrounding topics that we didn't fit into the video:https://www.3blue1brown.com/sridhars-corner/2018/4/17/wallis-product-supplement-dominated-convergenceSpecial thanks to the following Patreon supporters:http://3b1b.co/wallis-thanksIf you also want to support videos like these, visit https://www.patreon.com/3blue1brownAnother approach to this product by Johan Wästlund:http://www.math.chalmers.se/~wastlund/monthly.pdfWith more from Donald Knuth building off this idea:https://apetresc.wordpress.com/2010/12/28/knuths-why-pi-talk-at-stanford-part-1/Music by Vincent Rubinetti: https://vincerubinetti.bandcamp.com/album/the-music-of-3blue1brown------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted on new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: http://3b1b.co/recommendedVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3blue1brownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3blue1brown
2 Geometry
2.1 But why is a sphere's surface area four times its shadow?
The formula is no mere coincidence.Store: http://3b1b.co/storeHome page: https://www.3blue1brown.comSpecial thanks: http://3b1b.co/sphere-thanksDiscussion on Reddit: https://www.reddit.com/r/3Blue1Brown/comments/a2gqo0/but_why_is_a_spheres_surface_area_four_times_its/The first proof goes back to Greek times, due to Archimedes, who was charmed by the fact that a sphere has 2/3 the volume of a cylinder encompassing it, and 2/3 the surface area as well (if you consider the caps). Check out this video for another beautiful animation of that first proof:https://youtu.be/KZJw0AYn6_kCalculus series:http://3b1b.co/calculusThanks to these folks for letting me use their images at the end:https://www.youtube.com/user/vlogbrothershttps://www.youtube.com/user/physicswomanhttps://www.youtube.com/user/Vsaucehttps://www.youtube.com/user/onemeeeliondollars------------------These animations are largely made using manim, a scrappy open source python library: https://github.com/3b1b/manimIf you want to check it out, I feel compelled to warn you that it's not the most well-documented tool, and it has many other quirks you might expect in a library someone wrote with only their own use in mind.Music by Vincent Rubinetti.Download the music on Bandcamp:https://vincerubinetti.bandcamp.com/album/the-music-of-3blue1brownStream the music on Spotify:https://open.spotify.com/album/1dVyjwS8FBqXhRunaG5W5uIf you want to contribute translated subtitles or to help review those that have already been made by others and need approval, you can click the gear icon in the video and go to subtitles/cc, then "add subtitles/cc". I really appreciate those who do this, as it helps make the lessons accessible to more people.------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted on new videos, subscribe: http://3b1b.co/subscribeVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3blue1brownReddit: https://www.reddit.com/r/3blue1brownInstagram: https://www.instagram.com/3blue1brown_animations/Patreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brown
2.2 The hardest problem on the hardest test
A difficult geometry puzzle with an elegant solution.Home page: https://www.3blue1brown.com/Brought to you by you: http://3b1b.co/putnam-thanksAnd by Brilliant: https://brilliant.org/3b1bSolution to the puzzle mentioned at the end: https://brilliant.org/3b1bindicator/These videos exist thanks to Patreon:https://www.patreon.com/3blue1brownA different write-up of this solution:http://lsusmath.rickmabry.org/psisson/putnam/putnam-web.htm1992 Putnam with this problem:http://kskedlaya.org/putnam-archive/1992.pdfA problem with a similar flavor came up on the 2005 Putnam A6. Give it a try! The solution for that problem, by the way, was written by Calvin Lin, a friend of mine who works at Brilliant. Small world!http://kskedlaya.org/putnam-archive/2005.pdfhttp://kskedlaya.org/putnam-archive/2005s.pdf------------------Animations largely made using manim, a scrappy open source python library. https://github.com/3b1b/manimIf you want to check it out, I feel compelled to warn you that it's not the most well-documented tool, and has many other quirks you might expect in a library someone wrote with only their own use in mind.Music by Vincent Rubinetti.Download the music on Bandcamp:https://vincerubinetti.bandcamp.com/album/the-music-of-3blue1brownStream the music on Spotify:https://open.spotify.com/album/1dVyjwS8FBqXhRunaG5W5uIf you want to contribute translated subtitles or to help review those that have already been made by others and need approval, you can click the gear icon in the video and go to subtitles/cc, then "add subtitles/cc". I really appreciate those who do this, as it helps make the lessons accessible to more people.------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted on new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: http://3b1b.co/recommendedVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3Blue1BrownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3Blue1Brown
2.3 Who cares about topology? (Inscribed rectangle problem)
An unsolved conjecture, and a clever topological solution to a weaker version of the question.Brought to you by you: http://3b1b.co/topology-thanksHome page: https://www.3blue1brown.com/This video is based on a proof from H. Vaughan, 1977.You can see it written up (as a single rather-dense paragraph) here:http://topo.math.auburn.edu/tp/reprints/v06/tp06107.pdf------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted about new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: https://www.youtube.com/playlist?list=PLZHQObOWTQDPHP40bzkb0TKLRPwQGAoC-Various social media stuffs:Twitter: https://twitter.com/3Blue1BrownFacebook: https://www.facebook.com/3blue1brown/Reddit: https://www.reddit.com/r/3Blue1Brown
2.4 Ever wondered why slicing a cone gives an ellipse? It’s wonderfully clever!
Dandelin spheres, conic sections, and a view of genius in math.Brought to you by you: http://3b1b.co/dandelin-thanksHome page: https://www.3blue1brown.comThoughts on the recent change to be sponsor-free:https://www.patreon.com/posts/going-sponsor-19586800Video on Feynman's lost lecture: https://youtu.be/xdIjYBtnvZUI originally saw the proof of this video when I was reading Paul Lockhart's "Measurement", which I highly recommend to all math learners, young and old.New shirts/mugs available: http://3b1b.co/storeThe 3d animations in the video were done using Grapher, while 2d animations were done using https://github.com/3b1b/manimIf you want to contribute translated subtitles or to help review those that have already been made by others and need approval, you can click the gear icon in the video and go to subtitles/cc, then "add subtitles/cc". I really appreciate those who do this, as it helps make the lessons accessible to more people.Music by Vincent Rubinetti: https://vincerubinetti.bandcamp.com/album/the-music-of-3blue1brown------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted on new videos, subscribe: http://3b1b.co/subscribeVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3blue1brownReddit: https://www.reddit.com/r/3blue1brownInstagram: https://www.instagram.com/3blue1brown_animations/Patreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brown
2.5 Sneaky Topology | The Borsuk-Ulam theorem and stolen necklaces
Solving a discrete math puzzle using topology.Home page: https://www.3blue1brown.comBrought to you by you: http://3b1b.co/borsuk-thanksWant more fair division math fun? Check out this Mathologer videohttps://youtu.be/7s-YM-kcKME(Seriously, Mathologer is great)These videos are supported by the community.https://www.patreon.com/3blue1brownThe original 1986 by Alon and West with this proofhttps://m.tau.ac.il/~nogaa/PDFS/Publications/The%20Borsuk-Ulam%20Theorem%20and%20bisection%20of%20necklaces.pdfVSauce on fixed pointshttps://youtu.be/csInNn6pfT4EE Paper using ideas related to this puzzlehttps://dl.acm.org/citation.cfm?id=802179I first came across this paper thanks to Alon Amit's answer on this Quora posthttps://www.quora.com/As-of-2016-what-do-mathematicians-on-Quora-think-of-the-3Blue1Brown-maths-videosIf you want to contribute translated subtitles or to help review those that have already been made by others and need approval, you can click the gear icon in the video and go to subtitles/cc, then "add subtitles/cc". I really appreciate those who do this, as it helps make the lessons accessible to more people.Music by Vincent Rubinetti:https://vincerubinetti.bandcamp.com/album/the-music-of-3blue1brown------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted on new videos, subscribe: http://3b1b.co/subscribeVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3blue1brownReddit: https://www.reddit.com/r/3blue1brownInstagram: https://www.instagram.com/3blue1brown_animations/Patreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brown
2.6 Thinking outside the 10-dimensional box
Visualizing high-dimensional spheres to understand a surprising puzzle.Home page: https://www.3blue1brown.com/Brought to you by you: http://3b1b.co/high-d-thanksAnd by Brilliant: https://brilliant.org/3b1bPodcast! https://www.benbenandblue.com/Check out Ben Eater's channel: https://www.youtube.com/user/eaterbc------------------Animations largely made using manim, a scrappy open source python library. https://github.com/3b1b/manimIf you want to check it out, I feel compelled to warn you that it's not the most well-documented tool, and it has many other quirks you might expect in a library someone wrote with only their own use in mind.Music by Vincent Rubinetti.Download the music on Bandcamp:https://vincerubinetti.bandcamp.com/album/the-music-of-3blue1brownStream the music on Spotify:https://open.spotify.com/album/1dVyjwS8FBqXhRunaG5W5uIf you want to contribute translated subtitles or to help review those that have already been made by others and need approval, you can click the gear icon in the video and go to subtitles/cc, then "add subtitles/cc". I really appreciate those who do this, as it helps make the lessons accessible to more people.------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted on new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: http://3b1b.co/recommendedVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3Blue1BrownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3Blue1Brown
2.7 Circle Division Solution
An explanation of a neat circle puzzle involving combinatorics, graphs, Euler's characteristic formula and pascal's triangle.Typo: At 7:30, the second term at the very bottom should have "k-1" instead of "k"Music: Wyoming 307 by Time for Three
3 Differential equations
3.1 Differential equations, studying the unsolvable | DE1
An overview of what ODEs are all aboutHome page: https://3blue1brown.com/Brought to you by you: http://3b1b.co/de1thanksNeed to brush up on calculus? https://youtu.be/WUvTyaaNkzMError correction: At 6:27, the upper equation should have g/L instead of L/g.Steven Strogatz NYT article on the math of love:https://opinionator.blogs.nytimes.com/2009/05/26/guest-column-loves-me-loves-me-not-do-the-math/Interactive visualization of the example from this video, by Ilya Perederiy:https://www.expunctis.com/2019/04/04/vtvt-another-demo.htmlIf you're looking for books on this topic, I'd recommend the one by Vladimir Arnold, "Ordinary Differential Equations"Also, more Strogatz fun, you may enjoy his text "Nonlinear Dynamics And Chaos"Curious about why it's called a "phase space"? You might enjoy this article:https://www.physics.umd.edu/courses/Phys404/Anlage_Spring10/The%20TangledTaleofPhaseSpace.pdfFrom a response on /r/3blue1brown, here are some interactives based on examples shown in the video:https://observablehq.com/@tophtucker/tales-from-the-romeo-and-juliet-phase-spacehttps://observablehq.com/@mbostock/predator-and-prey------------------Animations made using manim, a scrappy open source python library. https://github.com/3b1b/manimIf you want to check it out, I feel compelled to warn you that it's not the most well-documented tool, and has many other quirks you might expect in a library someone wrote with only their own use in mind.Music by Vincent Rubinetti.Download the music on Bandcamp:https://vincerubinetti.bandcamp.com/album/the-music-of-3blue1brownStream the music on Spotify:https://open.spotify.com/album/1dVyjwS8FBqXhRunaG5W5uIf you want to contribute translated subtitles or to help review those that have already been made by others and need approval, you can click the gear icon in the video and go to subtitles/cc, then "add subtitles/cc". I really appreciate those who do this, as it helps make the lessons accessible to more people.------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted on new videos, subscribe: http://3b1b.co/subscribeVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3blue1brownReddit: https://www.reddit.com/r/3blue1brownInstagram: https://www.instagram.com/3blue1brown_animations/Patreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brown
3.2 But what is a partial differential equation? | DE2
The heat equation, as an introductory PDE.Home page: https://www.3blue1brown.comBrought to you by you: http://3b1b.co/de2thanksInfinite powers, by Steven Strogatz:https://www.amazon.com/Infinite-Powers-Calculus-Reveals-Universe/dp/1328879984Typo corrections:- At 1:33, it should be “Black-Scholes”- At 16:21 it should read "scratch an itch".If anyone asks, I purposefully leave at least one typo in each video, like a Navajo rug with a deliberate imperfection as an artistic statement about the nature of life ;)And to continue my unabashed Strogatz fanboyism, I should also mention that his textbook on nonlinear dynamics and chaos was also a meaningful motivator to do this series, as you'll hopefully see with the topics we build to.------------------Animations made using manim, a scrappy open source python library. https://github.com/3b1b/manimIf you want to check it out, I feel compelled to warn you that it's not the most well-documented tool, and has many other quirks you might expect in a library someone wrote with only their own use in mind.Music by Vincent Rubinetti.Download the music on Bandcamp:https://vincerubinetti.bandcamp.com/album/the-music-of-3blue1brownStream the music on Spotify:https://open.spotify.com/album/1dVyjwS8FBqXhRunaG5W5uIf you want to contribute translated subtitles or to help review those that have already been made by others and need approval, you can click the gear icon in the video and go to subtitles/cc, then "add subtitles/cc". I really appreciate those who do this, as it helps make the lessons accessible to more people.------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted on new videos, subscribe: http://3b1b.co/subscribeVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3blue1brownReddit: https://www.reddit.com/r/3blue1brownInstagram: https://www.instagram.com/3blue1brown_animations/Patreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brown
3.3 Solving the heat equation | DE3
Boundary conditions, and setup for how Fourier series are useful.Home page: https://www.3blue1brown.comBrought to you by you: http://3b1b.co/de3thanksMore about the heat equation, with a derivation in terms of slope corresponding to heat flow from MIT OCW:https://ocw.mit.edu/courses/mathematics/18-303-linear-partial-differential-equations-fall-2006/lecture-notes/heateqni.pdfIf you want to learn more about Fourier series, here are a few great videos/posts which I think you'll enjoy:Mathologer's: https://youtu.be/qS4H6PEcCCAThe Coding Train: https://youtu.be/Mm2eYfj0SgAJez Swanson: http://www.jezzamon.com/fourier/------------------These animations are largely made using manim, a scrappy open source python library: https://github.com/3b1b/manimIf you want to check it out, I feel compelled to warn you that it's not the most well-documented tool, and it has many other quirks you might expect in a library someone wrote with only their own use in mind.Music by Vincent Rubinetti.Download the music on Bandcamp:https://vincerubinetti.bandcamp.com/album/the-music-of-3blue1brownStream the music on Spotify:https://open.spotify.com/album/1dVyjwS8FBqXhRunaG5W5uIf you want to contribute translated subtitles or to help review those that have already been made by others and need approval, you can click the gear icon in the video and go to subtitles/cc, then "add subtitles/cc". I really appreciate those who do this, as it helps make the lessons accessible to more people.------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted on new videos, subscribe: http://3b1b.co/subscribeVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3blue1brownReddit: https://www.reddit.com/r/3blue1brownInstagram: https://www.instagram.com/3blue1brown_animations/Patreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brown
3.4 But what is a Fourier series? From heat flow to circle drawings | DE4
Fourier series, from the heat equation to sines to cycles.Home page: https://www.3blue1brown.comBrought to you by you: http://3b1b.co/de4thanks12 minutes of pure Fourier series animations: https://youtu.be/-qgreAUpPwMSome viewers made apps that create circle animations for your own drawing. Check them out!https://www.reddit.com/r/3Blue1Brown/comments/cvpdn7/make_your_own_fourier_circle_drawings/https://isaacvr.github.io/coding/fourier_transform/Thanks to Stuart@Biocinematics for the one-line sketch of Fourier via twitter. As it happens, he also has an educational YouTube channel:https://www.youtube.com/channel/UCKOiJd9YCbv7LeL2LFOGiLQSmall correction: at 9:33, all the exponents should have a pi^2 in them.If you're looking for more Fourier Series content online, including code to play with to create this kind of animation yourself, check out these posts:Mathologerhttps://youtu.be/qS4H6PEcCCAThe Coding Trainhttps://youtu.be/Mm2eYfj0SgAJezmoonhttp://www.jezzamon.com/fourier/index.htmlFor those of you into pure math looking to really dig into the analysis behind this topic, you might want to take a look at Stein Shakarchi's book "Fourier Analysis: An Introduction"------------------These animations are largely made using manim, a scrappy open source python library: https://github.com/3b1b/manimIf you want to check it out, I feel compelled to warn you that it's not the most well-documented tool, and it has many other quirks you might expect in a library someone wrote with only their own use in mind.Music by Vincent Rubinetti.Download the music on Bandcamp:https://vincerubinetti.bandcamp.com/album/the-music-of-3blue1brownStream the music on Spotify:https://open.spotify.com/album/1dVyjwS8FBqXhRunaG5W5uIf you want to contribute translated subtitles or to help review those that have already been made by others and need approval, you can click the gear icon in the video and go to subtitles/cc, then "add subtitles/cc". I really appreciate those who do this, as it helps make the lessons accessible to more people.------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted on new videos, subscribe: http://3b1b.co/subscribeVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3blue1brownReddit: https://www.reddit.com/r/3blue1brownInstagram: https://www.instagram.com/3blue1brown_animations/Patreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brown
3.5 Understanding e to the i pi in 3.14 minutes | DE5
Euler's formula intuition from relating velocities to positions.Home page: https://www.3blue1brown.comYeah yeah, the runtime is 4:08, but it's 3.14 minutes to the conclusion.Not familiar with the calculus referenced in this video? Try taking a look at this one:https://youtu.be/m2MIpDrF7EsAnother perspective on this formula, from Mathologer:https://youtu.be/-dhHrg-KbJ0Another perspective from this channel:https://youtu.be/mvmuCPvRoWQAnd yet another from the blog Better Explained:https://betterexplained.com/articles/intuitive-understanding-of-eulers-formula/I'm not sure where the perspective shown in this video originates. I do know you can find it in Tristan Needham's excellent book "Visual Complex Analysis", but if anyone has a sense of the first occurrence of this intuition do feel free to share. It's simple and natural enough, though, that it's probably a view which has been independently thought up many times over.------------------These animations are largely made using manim, a scrappy open source python library: https://github.com/3b1b/manimIf you want to check it out, I feel compelled to warn you that it's not the most well-documented tool, and it has many other quirks you might expect in a library someone wrote with only their own use in mind.Music by Vincent Rubinetti.Download the music on Bandcamp:https://vincerubinetti.bandcamp.com/album/the-music-of-3blue1brownStream the music on Spotify:https://open.spotify.com/album/1dVyjwS8FBqXhRunaG5W5uIf you want to contribute translated subtitles or to help review those that have already been made by others and need approval, you can click the gear icon in the video and go to subtitles/cc, then "add subtitles/cc". I really appreciate those who do this, as it helps make the lessons accessible to more people.------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted on new videos, subscribe: http://3b1b.co/subscribeVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3blue1brownReddit: https://www.reddit.com/r/3blue1brownInstagram: https://www.instagram.com/3blue1brown_animations/Patreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brown
4 The block collision puzzle
4.1 The most unexpected answer to a counting puzzle
If this doesn't blow your mind, I don't know what will.Part 2: https://youtu.be/jsYwFizhncEPart 3: https://youtu.be/brU5yLm9DZMBrought to you by you: http://3b1b.co/clacks-thanksNew to this channel? It's all about teaching math visually. Take a look and see if there's anything you'd like to learn.NY Times blog post about this problem:https://wordplay.blogs.nytimes.com/2014/03/10/pi/The original paper by Gregory Galperin:https://www.maths.tcd.ie/~lebed/Galperin.%20Playing%20pool%20with%20pi.pdfEvidently, Numberphile also described this problem (I had not known):https://youtu.be/abv4Fz7oNr0You'll notice that video has an added factor of 16 throughout, which is not here. That's because they're only counting the collisions between blocks (well, balls in their case), and they're only counting to the point where the big block starts moving the other way.------------------These animations are largely made using manim, a scrappy open source python library: https://github.com/3b1b/manimIf you want to check it out, I feel compelled to warn you that it's not the most well-documented tool, and it has many other quirks you might expect in a library someone wrote with only their own use in mind.Music by Vincent Rubinetti.Download the music on Bandcamp:https://vincerubinetti.bandcamp.com/album/the-music-of-3blue1brownStream the music on Spotify:https://open.spotify.com/album/1dVyjwS8FBqXhRunaG5W5uIf you want to contribute translated subtitles or to help review those that have already been made by others and need approval, you can click the gear icon in the video and go to subtitles/cc, then "add subtitles/cc". I really appreciate those who do this, as it helps make the lessons accessible to more people.------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted on new videos, subscribe: http://3b1b.co/subscribeVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3blue1brownReddit: https://www.reddit.com/r/3blue1brownInstagram: https://www.instagram.com/3blue1brown_animations/Patreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brown
4.2 Why do colliding blocks compute pi?
Part 1: https://youtu.be/HEfHFsfGXjsPart 3: https://youtu.be/brU5yLm9DZMHome page: https://www.3blue1brown.comBrought to you by you: http://3b1b.co/clacks-thanks Many of you shared solutions, attempts, and simulations with me this last week. I loved it! Y'all are the best. Here are just two of my favorites.By a channel STEM cell: https://youtu.be/ils7GZqp_iEBy Doga Kurkcuoglu: http://bilimneguzellan.net/bouncing-cubes-and-%CF%80-3blue1brown/And here's a lovely interactive built by GitHub user prajwalsouza after watching this video: https://prajwalsouza.github.io/Experiments/Colliding-Blocks.htmlNY Times blog post about this problem:https://wordplay.blogs.nytimes.com/2014/03/10/pi/The original paper by Gregory Galperin:https://www.maths.tcd.ie/~lebed/Galperin.%20Playing%20pool%20with%20pi.pdfFor anyone curious about if the tan(x) ≈ x approximation, being off by only a cubic error term, is actually close enough not to affect the final count, take a look at sections 9 and 10 of Galperin's paper. In short, it could break if there were some point where among the first 2N digits of pi, the last N of them were all 9's. This seems exceedingly unlikely, but it quite hard to disprove.Although I found the approach shown in this video independently, after the fact I found that Gary Antonick, who wrote the Numberplay blog referenced above, was the first to solve it this way. In some ways, I think this is the most natural approach one might take given the problem statement, as corroborated by the fact that many solutions people sent my way in this last week had this flavor. The Galperin solution you will see in the next video, though, involves a wonderfully creative perspective.If you want to contribute translated subtitles or to help review those that have already been made by others and need approval, you can click the gear icon in the video and go to subtitles/cc, then "add subtitles/cc". I really appreciate those who do this, as it helps make the lessons accessible to more people.Music by Vincent Rubinetti.Download the music on Bandcamp:https://vincerubinetti.bandcamp.com/album/the-music-of-3blue1brownStream the music on Spotify:https://open.spotify.com/album/1dVyjwS8FBqXhRunaG5W5u------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted on new videos, subscribe: http://3b1b.co/subscribeVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3blue1brownReddit: https://www.reddit.com/r/3blue1brownInstagram: https://www.instagram.com/3blue1brown_animations/Patreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brown
4.3 How colliding blocks act like a beam of light…to compute pi.
The third and final part of the block collision sequence.Part 1: https://youtu.be/HEfHFsfGXjsPart 2: https://youtu.be/jsYwFizhncEHome page: https://www.3blue1brown.comBrought to you by you: http://3b1b.co/clacks-thanksError correction: I wrote the answer as floor(pi/theta), when really it should be ceiling(pi/theta) - 1 t account for values of theta perfectly dividing pi. For example, the case of equal masses gives an angle of pi/4, and 3 total clacks.This beautiful result, and the solution shown here, are due to Gregory Galperin:https://www.maths.tcd.ie/~lebed/Galperin.%20Playing%20pool%20with%20pi.pdfAnd here's a lovely interactive built by GitHub user prajwalsouza after watching this video: https://prajwalsouza.github.io/Experiments/Colliding-Blocks.htmlSpeaking of looking glass universes...https://www.youtube.com/user/LookingGlassUniverseNY Times blog post about this problem:https://wordplay.blogs.nytimes.com/2014/03/10/pi/The plushie pi shown at the video's start:https://www.3blue1brown.com/storeIf you want to contribute translated subtitles or to help review those that have already been made by others and need approval, you can click the gear icon in the video and go to subtitles/cc, then "add subtitles/cc". I really appreciate those who do this, as it helps make the lessons accessible to more people.Music by Vincent Rubinetti.Download the music on Bandcamp:https://vincerubinetti.bandcamp.com/album/the-music-of-3blue1brownStream the music on Spotify:https://open.spotify.com/album/1dVyjwS8FBqXhRunaG5W5u------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted on new videos, subscribe: http://3b1b.co/subscribeVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3blue1brownReddit: https://www.reddit.com/r/3blue1brownInstagram: https://www.instagram.com/3blue1brown_animations/Patreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brown
5 Physics
5.1 Some light quantum mechanics (with minutephysics)
The math of superposition and quantum states.minutephysics channel: https://www.youtube.com/user/minutephysicsBrought to you by you: http://3b1b.co/light-quantum-thanksAnd by Brilliant: https://brilliant.org/3b1bHuge thanks to my friend Evan Miyazono, both for encouraging me to do this project, and for helping me understand many things along the way.This is a simple primer for how the math of quantum mechanics, specifically in the context of polarized light, relates to the math of classical waves, specifically classical electromagnetic waves.I will say, if you *do* want to go off and learn the math of quantum mechanics, you just can never have too much linear algebra, so check out the series I did at http://3b1b.co/essence-of-linear-algebraMistakes: As several astute commenters have pointed out, the force arrow is pointing the wrong way at 2:18. Thanks for the catch!*Note on conventions: Throughout this video, I use a single-headed right arrow to represent the horizontal direction. The standard in quantum mechanics is actually to use double-headed arrows for describing polarization states, while single-headed arrows are typically reserved for the context of spin.What's the difference? Well, using a double-headed arrow to represent the horizontal direction emphasizes that in a quantum mechanical context, there's no distinction between left and right. They each have the same measurable state: horizontal (e.g. they pass through horizontally oriented filters). Once you're in QM, these kets are typically vectors in a more abstract space where vectors are not necessarily spatial directions but instead represent any kind of state.Because of how I chose to motivate things with classical waves, where it makes sense for this arrow to represent a unit vector in the right direction, rather than the more abstract idea of a horizontal state vector, I chose to stick with the single-headed notation throughout, though this runs slightly against convention.Music by Vincent Rubinetti:https://vincerubinetti.bandcamp.com/album/the-music-of-3blue1brown------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted on new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: http://3b1b.co/recommendedVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3Blue1BrownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3Blue1Brown
5.2 The more general uncertainty principle, beyond quantum
The Heisenberg uncertainty principle is just one specific example of a much more general, relatable, non-quantum phenomenon.Brought to you by you: http://3b1b.co/uncertainty-thanksAnd by Art of Problem Solving: http://aops.com/3b1bFor more on quantum mechanical wave functions, I highly recommend this video by udiprod:https://youtu.be/p7bzE1E5PMYMinute physics on special relativity:https://youtu.be/1rLWVZVWfdYMain video on the Fourier transformhttps://youtu.be/spUNpyF58BYLouis de Broglie thesis: http://aflb.ensmp.fr/LDB-oeuvres/De_Broglie_Kracklauer.pdfMore on Doppler radar:Radar basics: https://www.eetimes.com/document.asp?doc_id=1278808There's a key way in which the description I gave of the trade-off in Doppler radar differs from reality. Since the speed of light is so drastically greater than the speed of things being detected, the Fourier representation for pulse echoes of different objects would almost certainly overlap unless it was played for a very long time. In effect, this is what happens, since one does not send out a single pulse, but a whole bunch of evenly spaced pulses as some pulse repetition frequency (or PRF). This means the Fourier representation of all those pulses together can actually be quite sharp. Assuming a large number of such pulses, it will look like several vertical lines spaced out by the PRF. As long as the pulses are far enough apart that the echoes of multiple objects on the field from different targets don't overlap, it's not a problem for position determinations that the full sequence of pulses occupies such a long duration. However, the trade-off now comes in choosing the right PRF. See the above article for more information.Music by Vincent Rubinetti: https://vincerubinetti.bandcamp.com/album/the-music-of-3blue1brown------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted on new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: http://3b1b.co/recommendedVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3Blue1BrownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3Blue1Brown
5.3 Feynman's Lost Lecture (ft. 3Blue1Brown)
Check out Grant’s channel: 3blue1brown: https://www.youtube.com/3blue1brownThis video recounts a lecture by Richard Feynman giving an elementary demonstration of why planets orbit in ellipses. See the excellent book by Judith and David Goodstein, "Feynman's lost lecture”, for the full story behind this lecture, and a deeper dive into its content.Tweet referenced at the start: https://twitter.com/3blue1brown/status/1016936129117937664Music by Nathaniel Schroeder: https://soundcloud.com/drschroeder/elizabeth-the-mouseMusic by Vincent Rubinetti: https://soundcloud.com/vincerubinetti/one-two-zetaSupport MinutePhysics on Patreon! http://www.patreon.com/minutephysicsLink to Patreon Supporters: http://www.minutephysics.com/supporters/MinutePhysics is on twitter - @minutephysicsAnd facebook - http://facebook.com/minutephysicsAnd Google+ (does anyone use this any more?) - http://bit.ly/qzEwc6Minute Physics provides an energetic and entertaining view of old and new problems in physics -- all in a minute!Created by Henry Reich
5.4 Visualizing turbulence
Some mathematical order amidst the chaos of turbulence.Vortex rings with Physics Girl: https://youtu.be/N7d_RWyOv20Brought to you by you: http://3b1b.co/turbulence-thanksHome page: https://www.3blue1brown.comThanks to Dan Walsh for many great ideas, and thanks to Mike Hansen for many helpful conversations.Error correction: I meant to describe Kolmogorov as a “20th-century mathematician” not “19th-century”. Whoops! I think during the narration I must have made the classic 1900s vs. 19th-century mix up. Anyone aware of his work is more than aware of what century he lived in, which apparently applies to quite a few commenters.And while we're here, the animation at 9:55 misleadingly has the vortex kind of speed up during the transition, which it should not do. Really, the velocity scales of eddies decreases for lower length scales.Introduction to turbulence:http://www.astronomy.ohio-state.edu/~ryden/ast825/ch7.pdfMore details on vortex stretching:https://www.math.nyu.edu/faculty/tabak/vorticity.pdfVideo on NightHawkInLight with a similar demo:https://youtu.be/K94Cc21KEIAMusic by Vincent Rubinetti: https://vincerubinetti.bandcamp.com/album/the-music-of-3blue1brown------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted on new videos, subscribe: http://3b1b.co/subscribeVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3blue1brownReddit: https://www.reddit.com/r/3blue1brownInstagram: https://www.instagram.com/3blue1brown_animations/Patreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brown
6 Neat proofs/perspectives
6.1 The hardest problem on the hardest test
A difficult geometry puzzle with an elegant solution.Home page: https://www.3blue1brown.com/Brought to you by you: http://3b1b.co/putnam-thanksAnd by Brilliant: https://brilliant.org/3b1bSolution to the puzzle mentioned at the end: https://brilliant.org/3b1bindicator/These videos exist thanks to Patreon:https://www.patreon.com/3blue1brownA different write-up of this solution:http://lsusmath.rickmabry.org/psisson/putnam/putnam-web.htm1992 Putnam with this problem:http://kskedlaya.org/putnam-archive/1992.pdfA problem with a similar flavor came up on the 2005 Putnam A6. Give it a try! The solution for that problem, by the way, was written by Calvin Lin, a friend of mine who works at Brilliant. Small world!http://kskedlaya.org/putnam-archive/2005.pdfhttp://kskedlaya.org/putnam-archive/2005s.pdf------------------Animations largely made using manim, a scrappy open source python library. https://github.com/3b1b/manimIf you want to check it out, I feel compelled to warn you that it's not the most well-documented tool, and has many other quirks you might expect in a library someone wrote with only their own use in mind.Music by Vincent Rubinetti.Download the music on Bandcamp:https://vincerubinetti.bandcamp.com/album/the-music-of-3blue1brownStream the music on Spotify:https://open.spotify.com/album/1dVyjwS8FBqXhRunaG5W5uIf you want to contribute translated subtitles or to help review those that have already been made by others and need approval, you can click the gear icon in the video and go to subtitles/cc, then "add subtitles/cc". I really appreciate those who do this, as it helps make the lessons accessible to more people.------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted on new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: http://3b1b.co/recommendedVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3Blue1BrownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3Blue1Brown
6.2 Why is pi here? And why is it squared? A geometric answer to the Basel problem
A most beautiful proof of the Basel problem, using light.Home page: https://www.3blue1brown.com/Brought to you by you: http://3b1b.co/basel-thanksAnd by Brilliant: https://brilliant.org/3b1bBrilliant's principles list that I referenced:https://brilliant.org/principles/Get early access and more through Patreon:https://www.patreon.com/3blue1brownThe content here was based on a paper by Johan Wästlundhttp://www.math.chalmers.se/~wastlund/Cosmic.pdfCheck out Mathologer's video on the many cousins of the Pythagorean theorem:https://youtu.be/p-0SOWbzUYIOn the topic of Mathologer, he also has a nice video about the Basel problem:https://youtu.be/yPl64xi_ZZAA simple Geogebra to play around with the Inverse Pythagorean Theorem argument shown here.https://ggbm.at/yPExUf7bSome of you may be concerned about the final step here where we said the circle approaches a line. What about all the lighthouses on the far end? Well, a more careful calculation will show that the contributions from those lights become more negligible. In fact, the contributions from almost all lights become negligible. For the ambitious among you, see this paper for full details.If you want to contribute translated subtitles or to help review those that have already been made by others and need approval, you can click the gear icon in the video and go to subtitles/cc, then "add subtitles/cc". I really appreciate those who do this, as it helps make the lessons accessible to more people.Music by Vincent Rubinetti: https://vincerubinetti.bandcamp.com/album/the-music-of-3blue1brown------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted on new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: http://3b1b.co/recommendedVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3Blue1BrownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3Blue1Brown
6.3 Who cares about topology? (Inscribed rectangle problem)
An unsolved conjecture, and a clever topological solution to a weaker version of the question.Brought to you by you: http://3b1b.co/topology-thanksHome page: https://www.3blue1brown.com/This video is based on a proof from H. Vaughan, 1977.You can see it written up (as a single rather-dense paragraph) here:http://topo.math.auburn.edu/tp/reprints/v06/tp06107.pdf------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted about new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: https://www.youtube.com/playlist?list=PLZHQObOWTQDPHP40bzkb0TKLRPwQGAoC-Various social media stuffs:Twitter: https://twitter.com/3Blue1BrownFacebook: https://www.facebook.com/3blue1brown/Reddit: https://www.reddit.com/r/3Blue1Brown
6.4 Euler's formula with introductory group theory
Intuition for e^(pi i) = -1, and an intro to group theory.Home page: https://www.3blue1brown.com/Brought to you by you: http://3b1b.co/epii-thanksAnd by the Emerald Cloud Lab:- Application software engineer: http://3b1b.co/ecl-app-se- Infrastructure engineer: http://3b1b.co/ecl-infra-se- Lab focused engineer: http://3b1b.co/ecl-lab-se- Scientific computing engineer: http://3b1b.co/ecl-sci-compThere's a slight mistake at 13:33, where the angle should be arctan(1/2) = 26.565 degrees, not 30 degrees. Arg! If anyone asks, I was just...er...rounding to the nearest 10's.For those looking to read more into group theory, I'm a fan of Keith Conrad's expository papers: http://www.math.uconn.edu/~kconrad/blurbs/------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted about new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: http://3b1b.co/recommendedVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3Blue1BrownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3Blue1Brown
6.5 All possible pythagorean triples, visualized
The pythagorean triples like (3, 4, 5), (5, 12, 13), etc. all follow a nice pattern which complex numbers expose in a beautiful way.Brought to you by you: http://3b1b.co/triples-thanksHome page: https://www.3blue1brown.com/And by Remix: https://www.remix.com/jobsRegarding the brief reference to Fermat's Last Theorem, what should be emphasized is that it refers to *positive* integers. You can of course have things like 0^3 + 2^3 = 2^3, or (-3)^3 + 3^3 = 0^3. Music by Vincent Rubinetti: https://vincerubinetti.bandcamp.com/album/the-music-of-3blue1brown------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted about new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: http://3b1b.co/recommendedVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3Blue1BrownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3Blue1Brown
6.6 But why is a sphere's surface area four times its shadow?
The formula is no mere coincidence.Store: http://3b1b.co/storeHome page: https://www.3blue1brown.comSpecial thanks: http://3b1b.co/sphere-thanksDiscussion on Reddit: https://www.reddit.com/r/3Blue1Brown/comments/a2gqo0/but_why_is_a_spheres_surface_area_four_times_its/The first proof goes back to Greek times, due to Archimedes, who was charmed by the fact that a sphere has 2/3 the volume of a cylinder encompassing it, and 2/3 the surface area as well (if you consider the caps). Check out this video for another beautiful animation of that first proof:https://youtu.be/KZJw0AYn6_kCalculus series:http://3b1b.co/calculusThanks to these folks for letting me use their images at the end:https://www.youtube.com/user/vlogbrothershttps://www.youtube.com/user/physicswomanhttps://www.youtube.com/user/Vsaucehttps://www.youtube.com/user/onemeeeliondollars------------------These animations are largely made using manim, a scrappy open source python library: https://github.com/3b1b/manimIf you want to check it out, I feel compelled to warn you that it's not the most well-documented tool, and it has many other quirks you might expect in a library someone wrote with only their own use in mind.Music by Vincent Rubinetti.Download the music on Bandcamp:https://vincerubinetti.bandcamp.com/album/the-music-of-3blue1brownStream the music on Spotify:https://open.spotify.com/album/1dVyjwS8FBqXhRunaG5W5uIf you want to contribute translated subtitles or to help review those that have already been made by others and need approval, you can click the gear icon in the video and go to subtitles/cc, then "add subtitles/cc". I really appreciate those who do this, as it helps make the lessons accessible to more people.------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted on new videos, subscribe: http://3b1b.co/subscribeVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3blue1brownReddit: https://www.reddit.com/r/3blue1brownInstagram: https://www.instagram.com/3blue1brown_animations/Patreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brown
6.7 What they won't teach you in calculus
A visual for derivatives which generalizes more nicely to topics beyond calculus.Brought to you by you: http://3b1b.co/alt-calc-thanksAnd by Brilliant: https://brilliant.org/3b1bHome page: https://www.3blue1brown.comEssence of calculus series:http://3b1b.co/calculusReally nice applet made based on this video by Reddit user Larconneur:https://www.geogebra.org/m/rftwacsyMusic by Vincent Rubinetti: https://vincerubinetti.bandcamp.com/album/the-music-of-3blue1brown------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted on new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: http://3b1b.co/recommendedVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3blue1brownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3blue1brown
6.8 Sneaky Topology | The Borsuk-Ulam theorem and stolen necklaces
Solving a discrete math puzzle using topology.Home page: https://www.3blue1brown.comBrought to you by you: http://3b1b.co/borsuk-thanksWant more fair division math fun? Check out this Mathologer videohttps://youtu.be/7s-YM-kcKME(Seriously, Mathologer is great)These videos are supported by the community.https://www.patreon.com/3blue1brownThe original 1986 by Alon and West with this proofhttps://m.tau.ac.il/~nogaa/PDFS/Publications/The%20Borsuk-Ulam%20Theorem%20and%20bisection%20of%20necklaces.pdfVSauce on fixed pointshttps://youtu.be/csInNn6pfT4EE Paper using ideas related to this puzzlehttps://dl.acm.org/citation.cfm?id=802179I first came across this paper thanks to Alon Amit's answer on this Quora posthttps://www.quora.com/As-of-2016-what-do-mathematicians-on-Quora-think-of-the-3Blue1Brown-maths-videosIf you want to contribute translated subtitles or to help review those that have already been made by others and need approval, you can click the gear icon in the video and go to subtitles/cc, then "add subtitles/cc". I really appreciate those who do this, as it helps make the lessons accessible to more people.Music by Vincent Rubinetti:https://vincerubinetti.bandcamp.com/album/the-music-of-3blue1brown------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted on new videos, subscribe: http://3b1b.co/subscribeVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3blue1brownReddit: https://www.reddit.com/r/3blue1brownInstagram: https://www.instagram.com/3blue1brown_animations/Patreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brown
6.9 Pi hiding in prime regularities
A story of pi, primes, complex numbers, and how number theory braids them together.Brought to you by you: http://3b1b.co/leibniz-thanksHome page: https://www.3blue1brown.com/And by Remix: https://www.remix.com/The fact that only primes that are one above a multiple of four can be expressed as the sum of two squares is known as "Fermat's theorem on sums of two squares": https://goo.gl/EdhaN2Music by Vince Rubinetti:https://vincerubinetti.bandcamp.com/album/the-music-of-3blue1brown------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted about new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: http://3b1b.co/recommendedVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3Blue1BrownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3Blue1Brown
6.10 Thinking outside the 10-dimensional box
Visualizing high-dimensional spheres to understand a surprising puzzle.Home page: https://www.3blue1brown.com/Brought to you by you: http://3b1b.co/high-d-thanksAnd by Brilliant: https://brilliant.org/3b1bPodcast! https://www.benbenandblue.com/Check out Ben Eater's channel: https://www.youtube.com/user/eaterbc------------------Animations largely made using manim, a scrappy open source python library. https://github.com/3b1b/manimIf you want to check it out, I feel compelled to warn you that it's not the most well-documented tool, and it has many other quirks you might expect in a library someone wrote with only their own use in mind.Music by Vincent Rubinetti.Download the music on Bandcamp:https://vincerubinetti.bandcamp.com/album/the-music-of-3blue1brownStream the music on Spotify:https://open.spotify.com/album/1dVyjwS8FBqXhRunaG5W5uIf you want to contribute translated subtitles or to help review those that have already been made by others and need approval, you can click the gear icon in the video and go to subtitles/cc, then "add subtitles/cc". I really appreciate those who do this, as it helps make the lessons accessible to more people.------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted on new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: http://3b1b.co/recommendedVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3Blue1BrownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3Blue1Brown
6.11 Ever wondered why slicing a cone gives an ellipse? It’s wonderfully clever!
Dandelin spheres, conic sections, and a view of genius in math.Brought to you by you: http://3b1b.co/dandelin-thanksHome page: https://www.3blue1brown.comThoughts on the recent change to be sponsor-free:https://www.patreon.com/posts/going-sponsor-19586800Video on Feynman's lost lecture: https://youtu.be/xdIjYBtnvZUI originally saw the proof of this video when I was reading Paul Lockhart's "Measurement", which I highly recommend to all math learners, young and old.New shirts/mugs available: http://3b1b.co/storeThe 3d animations in the video were done using Grapher, while 2d animations were done using https://github.com/3b1b/manimIf you want to contribute translated subtitles or to help review those that have already been made by others and need approval, you can click the gear icon in the video and go to subtitles/cc, then "add subtitles/cc". I really appreciate those who do this, as it helps make the lessons accessible to more people.Music by Vincent Rubinetti: https://vincerubinetti.bandcamp.com/album/the-music-of-3blue1brown------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted on new videos, subscribe: http://3b1b.co/subscribeVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3blue1brownReddit: https://www.reddit.com/r/3blue1brownInstagram: https://www.instagram.com/3blue1brown_animations/Patreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brown
6.12 The Brachistochrone, with Steven Strogatz
Steven Strogatz and I talk about a famous historical math problem, a clever solution, and a modern twist.------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted about new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: https://www.youtube.com/playlist?list=PLZHQObOWTQDPHP40bzkb0TKLRPwQGAoC-Various social media stuffs:Patreon: https://www.patreon.com/3blue1brownTwitter: https://twitter.com/3Blue1BrownFacebook: https://www.facebook.com/3blue1brown/Reddit: https://www.reddit.com/r/3Blue1Brown
6.13 Binary, Hanoi and Sierpinski, part 1
Binary counting can solve the towers of Hanoi puzzle, and if this isn't surprising enough, it can lead to a method for finding a curve that fills Sierpinski's triangle (which I get to in part 2).Thanks to Desmos for their help in supporting this video. They're hiring, and anyone interested should check out https://www.desmos.com/careersThanks to all Patreon supporters as well, you can support and get early access to future "Essence of" series here: https://www.patreon.com/3blue1brownI also want to give a special shoutout to the following patrons: CrypticSwarm, Ali Yahya, Dave Nicponski, Juan Batiz-Benet, Yu Jun, Othman Alikhan, Markus Persson, Joseph John Cox, Luc Ritchie, Einar Wikheim Johansen, Rish Kundalia, Achille Brighton, Kirk Werklund, Ripta Pasay, Felipe Diniz, Chris, Curtis Mitchell, Ari Royce, Bright , Myles Buckley, Robert P Zuckett, Andy Petsch, Otavio good, Karthik T, Steve Muench, Viesulas Sliupas, Steffen Persch, Brendan Shah, Andrew Mcnab, Matt Parlmer, Naoki Orai, Dan Davison, Jose Oscar Mur-Miranda, Aidan Boneham, Brent Kennedy, Henry Reich, Sean Bibby, Paul Constantine, Justin Clark, Mohannad Elhamod, Denis, Ben Granger, Jeffrey Herman, Jacob Young.
6.14 Binary, Hanoi, and Sierpinski, part 2
After seeing how binary counting can solve the towers of Hanoi puzzle in the last video, here we see how ternary counting solve a constrained version of the puzzle, and how this gives a way to walk through a Sierpinski triangle graph structure.Thanks to Desmos for their help in supporting this video. They're hiring, and anyone interested should check out https://www.desmos.com/careersThanks to all Patreon supporters as well, you can support and get early access to future "Essence of" series here: https://www.patreon.com/3blue1brownI also want to give a special shoutout to the following patrons: CrypticSwarm, Ali Yahya, Dave Nicponski, Juan Batiz-Benet, Yu Jun, Othman Alikhan, Markus Persson, Joseph John Cox, Luc Ritchie, Einar Wikheim Johansen, Rish Kundalia, Achille Brighton, Kirk Werklund, Ripta Pasay, Felipe Diniz, Chris, Curtis Mitchell, Ari Royce, Bright , Myles Buckley, Robert P Zuckett, Andy Petsch, Otavio good, Karthik T, Steve Muench, Viesulas Sliupas, Steffen Persch, Brendan Shah, Andrew Mcnab, Matt Parlmer, Naoki Orai, Dan Davison, Jose Oscar Mur-Miranda, Aidan Boneham, Brent Kennedy, Henry Reich, Sean Bibby, Paul Constantine, Justin Clark, Mohannad Elhamod, Denis, Ben Granger, Jeffrey Herman, Jacob Young.
6.15 Music And Measure Theory
A connection between a classical puzzle about rational numbers and what makes music harmonious.
6.16 Circle Division Solution
An explanation of a neat circle puzzle involving combinatorics, graphs, Euler's characteristic formula and pascal's triangle.Typo: At 7:30, the second term at the very bottom should have "k-1" instead of "k"Music: Wyoming 307 by Time for Three
6.17 Euler's Formula and Graph Duality
A description of planar graph duality, and how it can be applied in a particularly elegant proof of Euler's Characteristic Formula.Music: Wyoming 307 by Time For Three
7 Explainers
7.1 But what is the Fourier Transform? A visual introduction.
An animated introduction to the Fourier Transform.Home page: https://www.3blue1brown.com/Brought to you by you: http://3b1b.co/fourier-thanksFollow-on video about the uncertainty principle: https://youtu.be/MBnnXbOM5S4Interactive made by a viewer inspired by this video:https://prajwalsouza.github.io/Experiments/Fourier-Transform-Visualization.htmlAlso, take a look at this Jupyter notebook implementing this idea in a way you can play with:https://github.com/thatSaneKid/fourier/blob/master/Fourier%20Transform%20-%20A%20Visual%20Introduction.ipynb------------------Animations largely made using manim, a scrappy open-source python library. https://github.com/3b1b/manimIf you want to check it out, I feel compelled to warn you that it's not the most well-documented tool, and has many other quirks you might expect in a library someone wrote with only their own use in mind.Music by Vincent Rubinetti.Download the music on Bandcamp:https://vincerubinetti.bandcamp.com/album/the-music-of-3blue1brownStream the music on Spotify:https://open.spotify.com/album/1dVyjwS8FBqXhRunaG5W5uIf you want to contribute translated subtitles or to help review those that have already been made by others and need approval, you can click the gear icon in the video and go to subtitles/cc, then "add subtitles/cc". I really appreciate those who do this, as it helps make the lessons accessible to more people.------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted on new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: http://3b1b.co/recommendedVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3Blue1BrownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3Blue1Brown
7.2 But what is a Neural Network? | Deep learning, chapter 1
Home page: https://www.3blue1brown.com/Brought to you by you: http://3b1b.co/nn1-thanksAdditional funding provided by Amplify Partners For any early-stage ML entrepreneurs, Amplify would love to hear from you: 3blue1brown@amplifypartners.comFull playlist: http://3b1b.co/neural-networksTypo correction: At 14:45, the last index on the bias vector is n, when it's supposed to in fact be a k. Thanks for the sharp eyes that caught that!For those who want to learn more, I highly recommend the book by Michael Nielsen introducing neural networks and deep learning: https://goo.gl/ZmczdyThere are two neat things about this book. First, it's available for free, so consider joining me in making a donation Nielsen's way if you get something out of it. And second, it's centered around walking through some code and data which you can download yourself, and which covers the same example that I introduce in this video. Yay for active learning!https://github.com/mnielsen/neural-networks-and-deep-learningI also highly recommend Chris Olah's blog: http://colah.github.io/For more videos, Welch Labs also has some great series on machine learning: https://youtu.be/i8D90DkCLhIhttps://youtu.be/bxe2T-V8XRsFor those of you looking to go *even* deeper, check out the text "Deep Learning" by Goodfellow, Bengio, and Courville. Also, the publication Distill is just utterly beautiful: https://distill.pub/Lion photo by Kevin Pluck------------------Animations largely made using manim, a scrappy open source python library. https://github.com/3b1b/manimIf you want to check it out, I feel compelled to warn you that it's not the most well-documented tool, and has many other quirks you might expect in a library someone wrote with only their own use in mind.Music by Vincent Rubinetti.Download the music on Bandcamp:https://vincerubinetti.bandcamp.com/album/the-music-of-3blue1brownStream the music on Spotify:https://open.spotify.com/album/1dVyjwS8FBqXhRunaG5W5uIf you want to contribute translated subtitles or to help review those that have already been made by others and need approval, you can click the gear icon in the video and go to subtitles/cc, then "add subtitles/cc". I really appreciate those who do this, as it helps make the lessons accessible to more people.------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted on new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: http://3b1b.co/recommendedVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3Blue1BrownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3Blue1Brown
7.3 The Essence of Calculus, Chapter 1
What might it feel like to invent calculus?Brought to you by you: http://3b1b.co/eoc1-thanksHome page: https://www.3blue1brown.com/In this first video of the series, we see how unraveling the nuances of a simple geometry question can lead to integrals, derivatives, and the fundamental theorem of calculus.------------------These animations are largely made using manim, a scrappy open source python library: https://github.com/3b1b/manimIf you want to check it out, I feel compelled to warn you that it's not the most well-documented tool, and it has many other quirks you might expect in a library someone wrote with only their own use in mind.Music by Vincent Rubinetti.Download the music on Bandcamp:https://vincerubinetti.bandcamp.com/album/the-music-of-3blue1brownStream the music on Spotify:https://open.spotify.com/album/1dVyjwS8FBqXhRunaG5W5uIf you want to contribute translated subtitles or to help review those that have already been made by others and need approval, you can click the gear icon in the video and go to subtitles/cc, then "add subtitles/cc". I really appreciate those who do this, as it helps make the lessons accessible to more people.------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted about new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: http://3b1b.co/recommendedVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3Blue1BrownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3Blue1Brown
7.4 Vectors, what even are they? | Essence of linear algebra, chapter 1
Home page: https://www.3blue1brown.com/Kicking off the linear algebra lessons, let's make sure we're all on the same page about how specifically to think about vectors in this context.Typo correction: At 6:52, the screen shows[x1, y1] + [x2, y2] = [x1+y1, x2+y2]. Of course, this should actually be [x1, y1] + [x2, y2] = [x1+x2, y1+y2].Full series: http://3b1b.co/eolaFuture series like this are funded by the community, through Patreon, where supporters get early access as the series is being produced.http://3b1b.co/supportIf you want to contribute translated subtitles or to help review those that have already been made by others and need approval, you can click the gear icon in the video and go to subtitles/cc, then "add subtitles/cc". I really appreciate those who do this, as it helps make the lessons accessible to more people.Music: https://vincerubinetti.bandcamp.com/track/grants-etude------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted about new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: https://goo.gl/WmnCQZVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3Blue1BrownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3Blue1Brown
7.5 Visualizing the Riemann hypothesis and analytic continuation
Unraveling an enigmatic function.Home page: https://www.3blue1brown.com/Brought to you by you: http://3b1b.co/zeta-thanksPosters/shirts for this visualization at http://3b1b.co/storeMusic by Vince Rubinetti: https://soundcloud.com/vincerubinetti/riemann-zeta-functionCheck out some of Vince's other work here: http://www.vincentrubinetti.com/For those who want to learn more about complex exponentiation, here are a few resources:- My video on the topic: http://youtu.be/mvmuCPvRoWQ- Mathologer's: https://youtu.be/-dhHrg-KbJ0- Better Explained: https://goo.gl/z28x2RFor those who want to learn more about the relationship between 1+2+3+4+... and -1/12, I'm quite fond of this blog post by Terry Tao: https://goo.gl/XRzyTJAlso, in a different video "What does it feel like to invent math", I give a completely different example of how adding up growing positive numbers can meaningfully give a negative number, so long as you loosen your understanding of what distance should mean for numbers: https://youtu.be/XFDM1ip5HdUInterestingly, that vertical line where the convergent portion of the function appears to abruptly stop corresponds to numbers whose real part is Euler's constant, ~0.577. For those who know what this is, it's kind of fun to puzzle about why this is the case.------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted about new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: https://goo.gl/WmnCQZVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3Blue1BrownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3Blue1Brown
7.6 But how does bitcoin actually work?
The math behind cryptocurrencies.Home page: https://www.3blue1brown.com/Brought to you by you: http://3b1b.co/btc-thanksAnd by Protocol Labs: https://protocol.ai/join/Some people have asked if this channel accepts contributions in cryptocurrency form. As a matter of fact, it does:http://3b1b.co/crypto2^256 video: https://youtu.be/S9JGmA5_unYMusic by Vincent Rubinetti: https://soundcloud.com/vincerubinetti/heartbeatHere are a few other resources I'd recommend:Original Bitcoin paper: https://bitcoin.org/bitcoin.pdfBlock explorer: https://blockexplorer.com/Blog post by Michael Nielsen: https://goo.gl/BW1RV3(This is particularly good for understanding the details of what transactions look like, which is something this video did not cover)Video by CuriousInventor: https://youtu.be/Lx9zgZCMqXEVideo by Anders Brownworth: https://youtu.be/_160oMzblY8Ethereum white paper: https://goo.gl/XXZddT------------------Animations largely made using manim, a scrappy open source python library. https://github.com/3b1b/manimIf you want to check it out, I feel compelled to warn you that it's not the most well-documented tool, and has many other quirks you might expect in a library someone wrote with only their own use in mind.Music by Vincent Rubinetti.Download the music on Bandcamp:https://vincerubinetti.bandcamp.com/album/the-music-of-3blue1brownStream the music on Spotify:https://open.spotify.com/album/1dVyjwS8FBqXhRunaG5W5uIf you want to contribute translated subtitles or to help review those that have already been made by others and need approval, you can click the gear icon in the video and go to subtitles/cc, then "add subtitles/cc". I really appreciate those who do this, as it helps make the lessons accessible to more people.------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted on new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: http://3b1b.co/recommendedVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3Blue1BrownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3Blue1Brown
7.7 Some light quantum mechanics (with minutephysics)
The math of superposition and quantum states.minutephysics channel: https://www.youtube.com/user/minutephysicsBrought to you by you: http://3b1b.co/light-quantum-thanksAnd by Brilliant: https://brilliant.org/3b1bHuge thanks to my friend Evan Miyazono, both for encouraging me to do this project, and for helping me understand many things along the way.This is a simple primer for how the math of quantum mechanics, specifically in the context of polarized light, relates to the math of classical waves, specifically classical electromagnetic waves.I will say, if you *do* want to go off and learn the math of quantum mechanics, you just can never have too much linear algebra, so check out the series I did at http://3b1b.co/essence-of-linear-algebraMistakes: As several astute commenters have pointed out, the force arrow is pointing the wrong way at 2:18. Thanks for the catch!*Note on conventions: Throughout this video, I use a single-headed right arrow to represent the horizontal direction. The standard in quantum mechanics is actually to use double-headed arrows for describing polarization states, while single-headed arrows are typically reserved for the context of spin.What's the difference? Well, using a double-headed arrow to represent the horizontal direction emphasizes that in a quantum mechanical context, there's no distinction between left and right. They each have the same measurable state: horizontal (e.g. they pass through horizontally oriented filters). Once you're in QM, these kets are typically vectors in a more abstract space where vectors are not necessarily spatial directions but instead represent any kind of state.Because of how I chose to motivate things with classical waves, where it makes sense for this arrow to represent a unit vector in the right direction, rather than the more abstract idea of a horizontal state vector, I chose to stick with the single-headed notation throughout, though this runs slightly against convention.Music by Vincent Rubinetti:https://vincerubinetti.bandcamp.com/album/the-music-of-3blue1brown------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted on new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: http://3b1b.co/recommendedVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3Blue1BrownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3Blue1Brown
7.8 But what is a Fourier series? From heat flow to circle drawings | DE4
Fourier series, from the heat equation to sines to cycles.Home page: https://www.3blue1brown.comBrought to you by you: http://3b1b.co/de4thanks12 minutes of pure Fourier series animations: https://youtu.be/-qgreAUpPwMSome viewers made apps that create circle animations for your own drawing. Check them out!https://www.reddit.com/r/3Blue1Brown/comments/cvpdn7/make_your_own_fourier_circle_drawings/https://isaacvr.github.io/coding/fourier_transform/Thanks to Stuart@Biocinematics for the one-line sketch of Fourier via twitter. As it happens, he also has an educational YouTube channel:https://www.youtube.com/channel/UCKOiJd9YCbv7LeL2LFOGiLQSmall correction: at 9:33, all the exponents should have a pi^2 in them.If you're looking for more Fourier Series content online, including code to play with to create this kind of animation yourself, check out these posts:Mathologerhttps://youtu.be/qS4H6PEcCCAThe Coding Trainhttps://youtu.be/Mm2eYfj0SgAJezmoonhttp://www.jezzamon.com/fourier/index.htmlFor those of you into pure math looking to really dig into the analysis behind this topic, you might want to take a look at Stein Shakarchi's book "Fourier Analysis: An Introduction"------------------These animations are largely made using manim, a scrappy open source python library: https://github.com/3b1b/manimIf you want to check it out, I feel compelled to warn you that it's not the most well-documented tool, and it has many other quirks you might expect in a library someone wrote with only their own use in mind.Music by Vincent Rubinetti.Download the music on Bandcamp:https://vincerubinetti.bandcamp.com/album/the-music-of-3blue1brownStream the music on Spotify:https://open.spotify.com/album/1dVyjwS8FBqXhRunaG5W5uIf you want to contribute translated subtitles or to help review those that have already been made by others and need approval, you can click the gear icon in the video and go to subtitles/cc, then "add subtitles/cc". I really appreciate those who do this, as it helps make the lessons accessible to more people.------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted on new videos, subscribe: http://3b1b.co/subscribeVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3blue1brownReddit: https://www.reddit.com/r/3blue1brownInstagram: https://www.instagram.com/3blue1brown_animations/Patreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brown
7.9 Divergence and curl: The language of Maxwell's equations, fluid flow, and more
(See below for small-but-important error correction)More thoughts from the end: https://www.patreon.com/posts/19586800Special thanks: http://3b1b.co/divcurl-thanksError: At 4:55, the narration should say "counterclockwise rotation gives positive curl, clockwise rotation gives negative curl". The diagram is correct, though.My former work on divergence and curl at Khan Academy:https://www.khanacademy.org/math/multivariable-calculus/multivariable-derivativesFor more fun fluid-flow illustrations, which heavily influenced how I animated this video, I think you'll really enjoy this site: https://anvaka.github.io/fieldplay/Music by Vincent Rubinetti: https://vincerubinetti.bandcamp.com/album/the-music-of-3blue1brown------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted on new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: http://3b1b.co/recommendedVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3blue1brownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3blue1brown
7.10 Differential equations, studying the unsolvable | DE1
An overview of what ODEs are all aboutHome page: https://3blue1brown.com/Brought to you by you: http://3b1b.co/de1thanksNeed to brush up on calculus? https://youtu.be/WUvTyaaNkzMError correction: At 6:27, the upper equation should have g/L instead of L/g.Steven Strogatz NYT article on the math of love:https://opinionator.blogs.nytimes.com/2009/05/26/guest-column-loves-me-loves-me-not-do-the-math/Interactive visualization of the example from this video, by Ilya Perederiy:https://www.expunctis.com/2019/04/04/vtvt-another-demo.htmlIf you're looking for books on this topic, I'd recommend the one by Vladimir Arnold, "Ordinary Differential Equations"Also, more Strogatz fun, you may enjoy his text "Nonlinear Dynamics And Chaos"Curious about why it's called a "phase space"? You might enjoy this article:https://www.physics.umd.edu/courses/Phys404/Anlage_Spring10/The%20TangledTaleofPhaseSpace.pdfFrom a response on /r/3blue1brown, here are some interactives based on examples shown in the video:https://observablehq.com/@tophtucker/tales-from-the-romeo-and-juliet-phase-spacehttps://observablehq.com/@mbostock/predator-and-prey------------------Animations made using manim, a scrappy open source python library. https://github.com/3b1b/manimIf you want to check it out, I feel compelled to warn you that it's not the most well-documented tool, and has many other quirks you might expect in a library someone wrote with only their own use in mind.Music by Vincent Rubinetti.Download the music on Bandcamp:https://vincerubinetti.bandcamp.com/album/the-music-of-3blue1brownStream the music on Spotify:https://open.spotify.com/album/1dVyjwS8FBqXhRunaG5W5uIf you want to contribute translated subtitles or to help review those that have already been made by others and need approval, you can click the gear icon in the video and go to subtitles/cc, then "add subtitles/cc". I really appreciate those who do this, as it helps make the lessons accessible to more people.------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted on new videos, subscribe: http://3b1b.co/subscribeVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3blue1brownReddit: https://www.reddit.com/r/3blue1brownInstagram: https://www.instagram.com/3blue1brown_animations/Patreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brown
7.11 Fractals are typically not self-similar
An explanation of fractal dimension.Home page: https://www.3blue1brown.com/Brought to you by you: http://3b1b.co/fractals-thanksAnd by Affirm: https://www.affirm.com/Music by Vince Rubinetti: https://soundcloud.com/vincerubinetti/riemann-zeta-functionOne technical note: It's possible to have fractals with an integer dimension. The example to have in mind is some *very* rough curve, which just so happens to achieve roughness level exactly 2. Slightly rough might be around 1.1-dimension; quite rough could be 1.5; but a very rough curve could get up to 2.0 (or more). A classic example of this is the boundary of the Mandelbrot set. The Sierpinski pyramid also has dimension 2 (try computing it!).The proper definition of a fractal, at least as Mandelbrot wrote it, is a shape whose "Hausdorff dimension" is greater than its "topological dimension". Hausdorff dimension is similar to the box-counting one I showed in this video, in some sense counting using balls instead of boxes, and it coincides with box-counting dimension in many cases. But it's more general, at the cost of being a bit harder to describe. Topological dimension is something that's always an integer, wherein (loosely speaking) curve-ish things are 1-dimensional, surface-ish things are two-dimensional, etc. For example, a Koch Curve has topological dimension 1, and Hausdorff dimension 1.262. A rough surface might have topological dimension 2, but fractal dimension 2.3. And if a curve with topological dimension 1 has a Hausdorff dimension that *happens* to be exactly 2, or 3, or 4, etc., it would be considered a fractal, even though it's fractal dimension is an integer.See Mandelbrot's book "The Fractal Geometry of Nature" for the full details and more examples.------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted about new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: https://www.youtube.com/playlist?list=PLZHQObOWTQDPHP40bzkb0TKLRPwQGAoC-Various social media stuffs:Twitter: https://twitter.com/3Blue1BrownFacebook: https://www.facebook.com/3blue1brown/Reddit: https://www.reddit.com/r/3Blue1Brown
7.12 Visualizing quaternions (4d numbers) with stereographic projection
How to think about this 4d number system in our 3d space.Brought to you by you: http://3b1b.co/quaternion-thanksPart 2: https://youtu.be/zjMuIxRvygQInteractive version of these visuals: http://3imaginary1real.comQuanta article on quaternions:https://www.quantamagazine.org/the-strange-numbers-that-birthed-modern-algebra-20180906/The math of Alice in Wonderland:https://www.newscientist.com/article/mg20427391-600-alices-adventures-in-algebra-wonderland-solved/------------------If you want to contribute translated subtitles or to help review those that have already been made by others and need approval, you can click the gear icon in the video and go to subtitles/cc, then "add subtitles/cc". I really appreciate those who do this, as it helps make the lessons accessible to more people.Music by Vincent Rubinetti:https://vincerubinetti.bandcamp.com/album/the-music-of-3blue1brown------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted on new videos, subscribe: http://3b1b.co/subscribeVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3blue1brownReddit: https://www.reddit.com/r/3blue1brownInstagram: https://www.instagram.com/3blue1brown_animations/Patreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brown
7.13 The more general uncertainty principle, beyond quantum
The Heisenberg uncertainty principle is just one specific example of a much more general, relatable, non-quantum phenomenon.Brought to you by you: http://3b1b.co/uncertainty-thanksAnd by Art of Problem Solving: http://aops.com/3b1bFor more on quantum mechanical wave functions, I highly recommend this video by udiprod:https://youtu.be/p7bzE1E5PMYMinute physics on special relativity:https://youtu.be/1rLWVZVWfdYMain video on the Fourier transformhttps://youtu.be/spUNpyF58BYLouis de Broglie thesis: http://aflb.ensmp.fr/LDB-oeuvres/De_Broglie_Kracklauer.pdfMore on Doppler radar:Radar basics: https://www.eetimes.com/document.asp?doc_id=1278808There's a key way in which the description I gave of the trade-off in Doppler radar differs from reality. Since the speed of light is so drastically greater than the speed of things being detected, the Fourier representation for pulse echoes of different objects would almost certainly overlap unless it was played for a very long time. In effect, this is what happens, since one does not send out a single pulse, but a whole bunch of evenly spaced pulses as some pulse repetition frequency (or PRF). This means the Fourier representation of all those pulses together can actually be quite sharp. Assuming a large number of such pulses, it will look like several vertical lines spaced out by the PRF. As long as the pulses are far enough apart that the echoes of multiple objects on the field from different targets don't overlap, it's not a problem for position determinations that the full sequence of pulses occupies such a long duration. However, the trade-off now comes in choosing the right PRF. See the above article for more information.Music by Vincent Rubinetti: https://vincerubinetti.bandcamp.com/album/the-music-of-3blue1brown------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted on new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: http://3b1b.co/recommendedVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3Blue1BrownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3Blue1Brown
7.14 Hilbert's Curve: Is infinite math useful?
Space-filling curves, turning visual information into audio information, and the connection between infinite and finite math (this is a re-upload of an older video which had much worse audio).Supplement with more space-filling curve fun: https://youtu.be/RU0wScIj36oFor more information on sight-via sound, this paper involving rewiring a ferret's retinas to its auditory cortex is particularly thought-provoking: http://phy.ucsf.edu/~houde/coleman/sur2.pdfAlternatively, here is the NYT summary: https://goo.gl/qNuc14Also, check out this excellent podcast on Human echolocation: https://goo.gl/23f4YhFor anyone curious to read more about the connections between infinite and finite math, consider this Terry Tao blog post: https://goo.gl/NZ4yrWLion photo by Kevin PluckMusic by Vincent Rubinetti: https://vincerubinetti.bandcamp.com/album/the-music-of-3blue1brown------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted on new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: http://3b1b.co/recommendedVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3Blue1BrownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3Blue1Brownm/r/3Blue1Brown
8 Neural networks
8.1 But what is a Neural Network? | Deep learning, chapter 1
Home page: https://www.3blue1brown.com/Brought to you by you: http://3b1b.co/nn1-thanksAdditional funding provided by Amplify Partners For any early-stage ML entrepreneurs, Amplify would love to hear from you: 3blue1brown@amplifypartners.comFull playlist: http://3b1b.co/neural-networksTypo correction: At 14:45, the last index on the bias vector is n, when it's supposed to in fact be a k. Thanks for the sharp eyes that caught that!For those who want to learn more, I highly recommend the book by Michael Nielsen introducing neural networks and deep learning: https://goo.gl/ZmczdyThere are two neat things about this book. First, it's available for free, so consider joining me in making a donation Nielsen's way if you get something out of it. And second, it's centered around walking through some code and data which you can download yourself, and which covers the same example that I introduce in this video. Yay for active learning!https://github.com/mnielsen/neural-networks-and-deep-learningI also highly recommend Chris Olah's blog: http://colah.github.io/For more videos, Welch Labs also has some great series on machine learning: https://youtu.be/i8D90DkCLhIhttps://youtu.be/bxe2T-V8XRsFor those of you looking to go *even* deeper, check out the text "Deep Learning" by Goodfellow, Bengio, and Courville. Also, the publication Distill is just utterly beautiful: https://distill.pub/Lion photo by Kevin Pluck------------------Animations largely made using manim, a scrappy open source python library. https://github.com/3b1b/manimIf you want to check it out, I feel compelled to warn you that it's not the most well-documented tool, and has many other quirks you might expect in a library someone wrote with only their own use in mind.Music by Vincent Rubinetti.Download the music on Bandcamp:https://vincerubinetti.bandcamp.com/album/the-music-of-3blue1brownStream the music on Spotify:https://open.spotify.com/album/1dVyjwS8FBqXhRunaG5W5uIf you want to contribute translated subtitles or to help review those that have already been made by others and need approval, you can click the gear icon in the video and go to subtitles/cc, then "add subtitles/cc". I really appreciate those who do this, as it helps make the lessons accessible to more people.------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted on new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: http://3b1b.co/recommendedVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3Blue1BrownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3Blue1Brown
8.2 Gradient descent, how neural networks learn | Deep learning, chapter 2
Home page: https://www.3blue1brown.com/Brought to you by you: http://3b1b.co/nn2-thanksAnd by Amplify Partners.For any early stage ML startup founders, Amplify Partners would love to hear from you via 3blue1brown@amplifypartners.comTo learn more, I highly recommend the book by Michael Nielsenhttp://neuralnetworksanddeeplearning.com/The book walks through the code behind the example in these videos, which you can find here: https://github.com/mnielsen/neural-networks-and-deep-learningMNIST database:http://yann.lecun.com/exdb/mnist/Also check out Chris Olah's blog: http://colah.github.io/His post on Neural networks and topology is particular beautiful, but honestly all of the stuff there is great.And if you like that, you'll *love* the publications at distill:https://distill.pub/For more videos, Welch Labs also has some great series on machine learning: https://youtu.be/i8D90DkCLhIhttps://youtu.be/bxe2T-V8XRs"But I've already voraciously consumed Nielsen's, Olah's and Welch's works", I hear you say. Well well, look at you then. That being the case, I might recommend that you continue on with the book "Deep Learning" by Goodfellow, Bengio, and Courville.Thanks to Lisha Li (@lishali88) for her contributions at the end, and for letting me pick her brain so much about the material. Here are the articles she referenced at the end:https://arxiv.org/abs/1611.03530https://arxiv.org/abs/1706.05394https://arxiv.org/abs/1412.0233Music by Vincent Rubinetti: https://vincerubinetti.bandcamp.com/album/the-music-of-3blue1brown------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted on new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: http://3b1b.co/recommendedVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3Blue1BrownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3Blue1Brown
8.3 What is backpropagation really doing? | Deep learning, chapter 3
What's actually happening to a neural network as it learns?Next video: https://youtu.be/tIeHLnjs5U8Brought to you by you: http://3b1b.co/nn3-thanksAnd by CrowdFlower: http://3b1b.co/crowdflowerHome page: https://www.3blue1brown.com/The following video is sort of an appendix to this one. The main goal with the follow-on video is to show the connection between the visual walkthrough here, and the representation of these "nudges" in terms of partial derivatives that you will find when reading about backpropagation in other resources, like Michael Nielsen's book or Chis Olah's blog.
8.4 Backpropagation calculus | Deep learning, chapter 4
Brought to you by you: http://3b1b.co/nn3-thanksThis one is a bit more symbol heavy, and that's actually the point. The goal here is to represent in somewhat more formal terms the intuition for how backpropagation works in part 3 of the series, hopefully providing some connection between that video and other texts/code that you come across later.For more on backpropagation:http://neuralnetworksanddeeplearning.com/chap2.htmlhttps://github.com/mnielsen/neural-networks-and-deep-learninghttp://colah.github.io/posts/2015-08-Backprop/Music by Vincent Rubinetti:https://vincerubinetti.bandcamp.com/album/the-music-of-3blue1brown------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted on new videos, subscribe, and click the bell to receive notifications (if you're into that): http://3b1b.co/subscribeIf you are new to this channel and want to see more, a good place to start is this playlist: http://3b1b.co/recommendedVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3Blue1BrownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3Blue1Brown
9 Essence of calculus
9.1 The Essence of Calculus, Chapter 1
What might it feel like to invent calculus?Brought to you by you: http://3b1b.co/eoc1-thanksHome page: https://www.3blue1brown.com/In this first video of the series, we see how unraveling the nuances of a simple geometry question can lead to integrals, derivatives, and the fundamental theorem of calculus.------------------These animations are largely made using manim, a scrappy open source python library: https://github.com/3b1b/manimIf you want to check it out, I feel compelled to warn you that it's not the most well-documented tool, and it has many other quirks you might expect in a library someone wrote with only their own use in mind.Music by Vincent Rubinetti.Download the music on Bandcamp:https://vincerubinetti.bandcamp.com/album/the-music-of-3blue1brownStream the music on Spotify:https://open.spotify.com/album/1dVyjwS8FBqXhRunaG5W5uIf you want to contribute translated subtitles or to help review those that have already been made by others and need approval, you can click the gear icon in the video and go to subtitles/cc, then "add subtitles/cc". I really appreciate those who do this, as it helps make the lessons accessible to more people.------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted about new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: http://3b1b.co/recommendedVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3Blue1BrownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3Blue1Brown
9.2 The paradox of the derivative | Essence of calculus, chapter 2
Derivatives center on the idea of change in an instant, but change happens across time while an instant consists of just one moment. How does that work?Brought to you by you: http://3b1b.co/eoc2-thanksHome page: https://www.3blue1brown.com/And by Art of Problem Solving: https://aops.com/3blue1brownNote, to illustrate my point for the target audience of a new calculus student, I discussed a hypothetical speedometer that makes distance measurements over a very small time. Interestingly, most actual speedometers in modern cars work by analyzing the induced current of a spinning magnet, which is in some sense the universe implementing the derivative.------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted about new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: http://3b1b.co/recommendedVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3Blue1BrownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3Blue1Brown
9.3 Derivative formulas through geometry | Essence of calculus, chapter 3
A few derivative formulas, such as the power rule and the derivative of sine, demonstrated with geometric intuition.Brought to you by you: http://3b1b.co/eoc3-thanksAnd by Brilliant: https://brilliant.org/3b1bGreat video by Think Twice showing this geometric view of the derivative of sin(x):https://youtu.be/R4o7sraVMZgMusic:https://vincerubinetti.bandcamp.com/album/the-music-of-3blue1brown------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted about new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: http://3b1b.co/recommendedVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3Blue1BrownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3Blue1Brown
9.4 Visualizing the chain rule and product rule | Essence of calculus, chapter 4
A visual explanation of what the chain rule and product rule are, and why they are true.Full series: http://3b1b.co/calculusBrought to you by you: http://3b1b.co/eoc4-thanksAnd by Brilliant: https://brilliant.org/3b1bSeries like this one are funded largely by the community, through Patreon, where supporters get early access as the series is being produced.http://3b1b.co/support------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted about new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: http://3b1b.co/recommendedVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3Blue1BrownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3Blue1Brown
9.5 What's so special about Euler's number e? | Essence of calculus, chapter 5
What is e? And why are exponentials proportional to their own derivatives?Full series: http://3b1b.co/calculusBrought to you by you: http://3b1b.co/eoc5-thanksSupporters often get early access as the series like this: http://3b1b.co/support------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted about new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: http://3b1b.co/recommendedVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3Blue1BrownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3Blue1Brown
9.6 Implicit differentiation, what's going on here? | Essence of calculus, chapter 6
Implicit differentiation can feel weird, but what's going on makes much more sense once you view each side of the equation as a two-variable function, f(x, y).Brought to you by you: http://3b1b.co/eoc6-thanksFull series: http://3b1b.co/calculusSeries like this one are funded largely by the community, through Patreon, where supporters get early access as the series is being produced.http://3b1b.co/support------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted about new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: http://3b1b.co/recommendedVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3Blue1BrownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3Blue1Brown
9.7 Limits, L'Hopital's rule, and epsilon delta definitions | Essence of calculus, chapter 7
Formal derivatives, the epsilon-delta definition, and why L'Hôpital's rule works.Brought to you by you: http://3b1b.co/eoc7-thanksFull series: http://3b1b.co/calculusSeries like this one are funded largely by the community, through Patreon, where supporters get early access as the series is being produced.http://3b1b.co/support------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted about new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: http://3b1b.co/recommendedVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3Blue1BrownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3Blue1Brown
9.8 Integration and the fundamental theorem of calculus | Essence of calculus, chapter 8
What is an integral? How do you think about it?Check out the Art of Problem Solving: https://aops.com/3blue1brownFull series: http://3b1b.co/calculusSeries like this one are funded largely by the community, through Patreon, where supporters get early access as the series is being produced.http://3b1b.co/supportSpecial thanks to the following patrons: http://3b1b.co/eoc8-thanks------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted about new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: http://3b1b.co/recommendedVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3Blue1BrownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3Blue1Brown
9.9 What does area have to do with slope? | Essence of calculus, chapter 9
Integrals are used to find the average of a continuous variable, and this can offer a perspective on why integrals and derivatives are inverses, distinct from the one shown in the last video.Full series: http://3b1b.co/calculusSeries like this one are funded largely by the community, through Patreon, where supporters get early access as the series is being produced.http://3b1b.co/supportSpecial thanks to the following supporters: http://3b1b.co/eoc9-thanks------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted about new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: http://3b1b.co/recommendedVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3Blue1BrownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3Blue1Brown
9.10 Higher order derivatives | Essence of calculus, chapter 10
A very quick primer on the second derivative, third derivative, etc.Full playlist: http://3b1b.co/calculus------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted about new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: http://3b1b.co/recommendedVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3Blue1BrownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3Blue1Brown
9.11 Taylor series | Essence of calculus, chapter 11
Taylor polynomials are incredibly powerful for approximations, and Taylor series can give new ways to express functions.Brought to you by you: http://3b1b.co/eoc1-thanksHome page: https://www.3blue1brown.com/Full series: http://3b1b.co/calculusSeries like this one are funded largely by the community, through Patreon, where supporters get early access as the series is being produced.http://3b1b.co/support------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted about new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: http://3b1b.co/recommendedVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3Blue1BrownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3Blue1Brown
9.12 What they won't teach you in calculus
A visual for derivatives which generalizes more nicely to topics beyond calculus.Brought to you by you: http://3b1b.co/alt-calc-thanksAnd by Brilliant: https://brilliant.org/3b1bHome page: https://www.3blue1brown.comEssence of calculus series:http://3b1b.co/calculusReally nice applet made based on this video by Reddit user Larconneur:https://www.geogebra.org/m/rftwacsyMusic by Vincent Rubinetti: https://vincerubinetti.bandcamp.com/album/the-music-of-3blue1brown------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted on new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: http://3b1b.co/recommendedVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3blue1brownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3blue1brown
10 Binary, Hanoi and Sierpinski
10.1 Binary, Hanoi and Sierpinski, part 1
Binary counting can solve the towers of Hanoi puzzle, and if this isn't surprising enough, it can lead to a method for finding a curve that fills Sierpinski's triangle (which I get to in part 2).Thanks to Desmos for their help in supporting this video. They're hiring, and anyone interested should check out https://www.desmos.com/careersThanks to all Patreon supporters as well, you can support and get early access to future "Essence of" series here: https://www.patreon.com/3blue1brownI also want to give a special shoutout to the following patrons: CrypticSwarm, Ali Yahya, Dave Nicponski, Juan Batiz-Benet, Yu Jun, Othman Alikhan, Markus Persson, Joseph John Cox, Luc Ritchie, Einar Wikheim Johansen, Rish Kundalia, Achille Brighton, Kirk Werklund, Ripta Pasay, Felipe Diniz, Chris, Curtis Mitchell, Ari Royce, Bright , Myles Buckley, Robert P Zuckett, Andy Petsch, Otavio good, Karthik T, Steve Muench, Viesulas Sliupas, Steffen Persch, Brendan Shah, Andrew Mcnab, Matt Parlmer, Naoki Orai, Dan Davison, Jose Oscar Mur-Miranda, Aidan Boneham, Brent Kennedy, Henry Reich, Sean Bibby, Paul Constantine, Justin Clark, Mohannad Elhamod, Denis, Ben Granger, Jeffrey Herman, Jacob Young.
10.2 Binary, Hanoi, and Sierpinski, part 2
After seeing how binary counting can solve the towers of Hanoi puzzle in the last video, here we see how ternary counting solve a constrained version of the puzzle, and how this gives a way to walk through a Sierpinski triangle graph structure.Thanks to Desmos for their help in supporting this video. They're hiring, and anyone interested should check out https://www.desmos.com/careersThanks to all Patreon supporters as well, you can support and get early access to future "Essence of" series here: https://www.patreon.com/3blue1brownI also want to give a special shoutout to the following patrons: CrypticSwarm, Ali Yahya, Dave Nicponski, Juan Batiz-Benet, Yu Jun, Othman Alikhan, Markus Persson, Joseph John Cox, Luc Ritchie, Einar Wikheim Johansen, Rish Kundalia, Achille Brighton, Kirk Werklund, Ripta Pasay, Felipe Diniz, Chris, Curtis Mitchell, Ari Royce, Bright , Myles Buckley, Robert P Zuckett, Andy Petsch, Otavio good, Karthik T, Steve Muench, Viesulas Sliupas, Steffen Persch, Brendan Shah, Andrew Mcnab, Matt Parlmer, Naoki Orai, Dan Davison, Jose Oscar Mur-Miranda, Aidan Boneham, Brent Kennedy, Henry Reich, Sean Bibby, Paul Constantine, Justin Clark, Mohannad Elhamod, Denis, Ben Granger, Jeffrey Herman, Jacob Young.
11 Essence of linear algebra
11.1 Vectors, what even are they? | Essence of linear algebra, chapter 1
Home page: https://www.3blue1brown.com/Kicking off the linear algebra lessons, let's make sure we're all on the same page about how specifically to think about vectors in this context.Typo correction: At 6:52, the screen shows[x1, y1] + [x2, y2] = [x1+y1, x2+y2]. Of course, this should actually be [x1, y1] + [x2, y2] = [x1+x2, y1+y2].Full series: http://3b1b.co/eolaFuture series like this are funded by the community, through Patreon, where supporters get early access as the series is being produced.http://3b1b.co/supportIf you want to contribute translated subtitles or to help review those that have already been made by others and need approval, you can click the gear icon in the video and go to subtitles/cc, then "add subtitles/cc". I really appreciate those who do this, as it helps make the lessons accessible to more people.Music: https://vincerubinetti.bandcamp.com/track/grants-etude------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted about new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: https://goo.gl/WmnCQZVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3Blue1BrownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3Blue1Brown
11.2 Linear combinations, span, and basis vectors | Essence of linear algebra, chapter 2
Home page: https://www.3blue1brown.com/The fundamental vector concepts of span, linear combinations, linear dependence, and bases all center on one surprisingly important operation: Scaling several vectors and adding them together.Full series: http://3b1b.co/eolaFuture series like this are funded by the community, through Patreon, where supporters get early access as the series is being produced.http://3b1b.co/support------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted about new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: https://goo.gl/WmnCQZVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3Blue1BrownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3Blue1Brown
11.3 Linear transformations and matrices | Essence of linear algebra, chapter 3
Home page: https://www.3blue1brown.com/Matrices can be thought of as transforming space, and understanding how this work is crucial for understanding many other ideas that follow in linear algebra.Full series: http://3b1b.co/eolaFuture series like this are funded by the community, through Patreon, where supporters get early access as the series is being produced.http://3b1b.co/support------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted about new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: https://goo.gl/WmnCQZVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3Blue1BrownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3Blue1Brown
11.4 Matrix multiplication as composition | Essence of linear algebra, chapter 4
Home page: https://www.3blue1brown.com/Multiplying two matrices represents applying one transformation after another. Many facts about matrix multiplication become much clearer once you digest this fact.Full series: http://3b1b.co/eolaFuture series like this are funded by the community, through Patreon, where supporters get early access as the series is being produced.http://3b1b.co/support------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted about new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: https://goo.gl/WmnCQZVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3Blue1BrownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3Blue1Brown
11.5 Three-dimensional linear transformations | Essence of linear algebra, chapter 5
Home page: https://www.3blue1brown.com/What do 3d linear transformations look like? Having talked about the relationship between matrices and transformations in the last two videos, this one extends those same concepts to three dimensions.Full series: http://3b1b.co/eolaFuture series like this are funded by the community, through Patreon, where supporters get early access as the series is being produced.http://3b1b.co/support------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted about new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: https://goo.gl/WmnCQZVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3Blue1BrownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3Blue1Brown
11.6 The determinant | Essence of linear algebra, chapter 6
Home page: https://www.3blue1brown.com/The determinant of a linear transformation measures how much areas/volumes change during the transformation.Full series: http://3b1b.co/eolaFuture series like this are funded by the community, through Patreon, where supporters get early access as the series is being produced.http://3b1b.co/support------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted about new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: https://goo.gl/WmnCQZVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3Blue1BrownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3Blue1Brown
11.7 Inverse matrices, column space and null space | Essence of linear algebra, chapter 7
Home page: https://www.3blue1brown.com/How to think about linear systems of equations geometrically. The focus here is on gaining an intuition for the concepts of inverse matrices, column space, rank and null space, but the computation of those constructs is not discussed.Full series: http://3b1b.co/eolaFuture series like this are funded by the community, through Patreon, where supporters get early access as the series is being produced.http://3b1b.co/support------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted about new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: https://goo.gl/WmnCQZVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3Blue1BrownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3Blue1Brown
11.8 Nonsquare matrices as transformations between dimensions | Essence of linear algebra, chapter 8
Home page: https://www.3blue1brown.com/Because people asked, this is a video briefly showing the geometric interpretation of non-square matrices as linear transformations that go between dimensions.Full series: http://3b1b.co/eolaFuture series like this are funded by the community, through Patreon, where supporters get early access as the series is being produced.http://3b1b.co/support------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted about new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: https://goo.gl/WmnCQZVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3Blue1BrownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3Blue1Brown
11.9 Dot products and duality | Essence of linear algebra, chapter 9
Home page: https://www.3blue1brown.com/Dot products are a nice geometric tool for understanding projection. But now that we know about linear transformations, we can get a deeper feel for what's going on with the dot product, and the connection between its numerical computation and its geometric interpretation.Full series: http://3b1b.co/eolaFuture series like this are funded by the community, through Patreon, where supporters get early access as the series is being produced.http://3b1b.co/support------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted about new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: https://goo.gl/WmnCQZVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3Blue1BrownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3Blue1Brown
11.10 Cross products | Essence of linear algebra, Chapter 10
Home page: https://www.3blue1brown.com/This covers the main geometric intuition behind the 2d and 3d cross products.*Note, in all the computations here, I list the coordinates of the vectors as columns of a matrix, but many textbooks put them in the rows of a matrix instead. It makes no difference for the result, since the determinant is unchanged after a transpose, but given how I've framed most of this series I think it is more intuitive to go with a column-centric approach.Full series: http://3b1b.co/eolaFuture series like this are funded by the community, through Patreon, where supporters get early access as the series is being produced.http://3b1b.co/support------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted about new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: https://goo.gl/WmnCQZVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3Blue1BrownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3Blue1Brown
11.11 Cross products in the light of linear transformations | Essence of linear algebra chapter 11
Home page: https://www.3blue1brown.com/For anyone who wants to understand the cross product more deeply, this video shows how it relates to a certain linear transformation via duality. This perspective gives a very elegant explanation of why the traditional computation of a dot product corresponds to its geometric interpretation.*Note, in all the computations here, I list the coordinates of the vectors as columns of a matrix, but many textbooks put them in the rows of a matrix instead. It makes no difference for the result since the determinant is unchanged after a transpose, but given how I've framed most of this series I think it is more intuitive to go with a column-centric approach.Full series: http://3b1b.co/eolaFuture series like this are funded by the community, through Patreon, where supporters get early access as the series is being produced.http://3b1b.co/support------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted about new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: https://goo.gl/WmnCQZVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3Blue1BrownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3Blue1Brown
11.12 Cramer's rule, explained geometrically | Essence of linear algebra, chapter 12
This rule seems random to many students, but it has a beautiful reason for being true.Home page: https://www.3blue1brown.com/Brought to you by you: http://3b1b.co/cramer-thanksFull series: http://3b1b.co/eola----If you want to contribute translated subtitles or to help review those that have already been made by others and need approval, you can click the gear icon in the video and go to subtitles/cc, then "add subtitles/cc". I really appreciate those who do this, as it helps make the lessons accessible to more people.Music by Vincent Rubinetti.Download the music on Bandcamp:https://vincerubinetti.bandcamp.com/album/the-music-of-3blue1brownStream the music on Spotify:https://open.spotify.com/album/1dVyjwS8FBqXhRunaG5W5u------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted on new videos, subscribe: http://3b1b.co/subscribeVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3blue1brownReddit: https://www.reddit.com/r/3blue1brownInstagram: https://www.instagram.com/3blue1brown_animations/Patreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brown
11.13 Change of basis | Essence of linear algebra, chapter 13
Home page: https://www.3blue1brown.com/How do you translate back and forth between coordinate systems that use different basis vectors?Full series: http://3b1b.co/eolaFuture series like this are funded by the community, through Patreon, where supporters get early access as the series is being produced.http://3b1b.co/support
11.14 Eigenvectors and eigenvalues | Essence of linear algebra, chapter 14
Home page: https://www.3blue1brown.com/A visual understanding of eigenvectors, eigenvalues, and the usefulness of an eigenbasis.Full series: http://3b1b.co/eolaFuture series like this are funded by the community, through Patreon, where supporters get early access as the series is being produced.http://3b1b.co/supportTypo: At 12:27, "more that a line full" should be "more than a line full".------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted about new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: https://goo.gl/WmnCQZVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3Blue1BrownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3Blue1Brown
11.15 Abstract vector spaces | Essence of linear algebra, chapter 15
Home page: https://www.3blue1brown.com/The tools of linear algebra are extremely general, applying not just to the familiar vectors that we picture as arrows in space, but to all sorts of mathematical objects, like functions. This generality is captured with the notion of an abstract vector space.Full series: http://3b1b.co/eolaFuture series like this are funded by the community, through Patreon, where supporters get early access as the series is being produced.http://3b1b.co/support------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted about new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: https://goo.gl/WmnCQZVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3Blue1BrownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3Blue1Brown
12 Shorter videos
12.1 The most unexpected answer to a counting puzzle
If this doesn't blow your mind, I don't know what will.Part 2: https://youtu.be/jsYwFizhncEPart 3: https://youtu.be/brU5yLm9DZMBrought to you by you: http://3b1b.co/clacks-thanksNew to this channel? It's all about teaching math visually. Take a look and see if there's anything you'd like to learn.NY Times blog post about this problem:https://wordplay.blogs.nytimes.com/2014/03/10/pi/The original paper by Gregory Galperin:https://www.maths.tcd.ie/~lebed/Galperin.%20Playing%20pool%20with%20pi.pdfEvidently, Numberphile also described this problem (I had not known):https://youtu.be/abv4Fz7oNr0You'll notice that video has an added factor of 16 throughout, which is not here. That's because they're only counting the collisions between blocks (well, balls in their case), and they're only counting to the point where the big block starts moving the other way.------------------These animations are largely made using manim, a scrappy open source python library: https://github.com/3b1b/manimIf you want to check it out, I feel compelled to warn you that it's not the most well-documented tool, and it has many other quirks you might expect in a library someone wrote with only their own use in mind.Music by Vincent Rubinetti.Download the music on Bandcamp:https://vincerubinetti.bandcamp.com/album/the-music-of-3blue1brownStream the music on Spotify:https://open.spotify.com/album/1dVyjwS8FBqXhRunaG5W5uIf you want to contribute translated subtitles or to help review those that have already been made by others and need approval, you can click the gear icon in the video and go to subtitles/cc, then "add subtitles/cc". I really appreciate those who do this, as it helps make the lessons accessible to more people.------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted on new videos, subscribe: http://3b1b.co/subscribeVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3blue1brownReddit: https://www.reddit.com/r/3blue1brownInstagram: https://www.instagram.com/3blue1brown_animations/Patreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brown
12.2 How secure is 256 bit security?
Supplement to the cryptocurrency video: How hard is it to find a 256-bit hash just by guessing and checking? What kind of computer would that take?Cryptocurrency video: https://youtu.be/bBC-nXj3Ng4Home page: https://www.3blue1brown.com/Several people have commented about how 2^256 would be the maximum number of attempts, not the average. This depends on the thing being attempted. If it's guessing a private key, you are correct, but for something like guessing which input to a hash function gives the desired output (as in bitcoin mining, for example), which is the kind of thing I had in mind here, 2^256 would indeed be the average number of attempts needed, at least for a true cryptographic hash function. Think of rolling a die until you get a 6, how many rolls do you need to make, on average?Music by Vince Rubinetti:https://vincerubinetti.bandcamp.com/album/the-music-of-3blue1brown------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted on new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: http://3b1b.co/recommendedVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3Blue1BrownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3Blue1Brown
12.3 How pi was almost 6.283185…
Happy pi day! Did you know that in some of his notes, Euler used the symbol pi to represent 6.28..., before the more familiar 3.14... took off as a standard?Home page: https://www.3blue1brown.comPlushie creatures now available: http://3b1b.co/storeThe idea for this video, as well as the live shots, came from Ben Hambrecht, with the writing and animating done by Grant Sanderson. Special thanks to: - University Library Basel, for letting us rummage through their historical collection - Martin Mattmüller from the Bernoulli-Euler center for helpful discussion - Michael Hartl, author of the Tau Manifesto, for pointing us to obscure references - Library of the Institut de FranceCinematographer: Eugen HellerMusic by Vincent Rubinetti: https://vincerubinetti.bandcamp.com/album/the-music-of-3blue1brown------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted on new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: http://3b1b.co/recommendedVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3Blue1BrownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3Blue1Brown
12.4 Triangle of Power
In math, exponents, logarithms, and roots all circle around the same idea, but the notation for each varies radically. The triangle of power is an alternate notation, which I find to be absolutely beautiful.(This is the corrected version of the one I put out a month or so ago, in which my animation for all the inverse operations was incorrect)Here's a sketch from the math redditer Cosmologicon showing how this might be usual with practical space considerations: http://i.imgur.com/hAeJokq.jpgThis original comes from an answer to a math exchange post by Alex Jordan, which you can find here: http://math.stackexchange.com/questions/30046/alternative-notation-for-exponents-logs-and-rootsI also briefly flashed a blog post with another interesting alternative for logarithm notation: http://www.solidangl.es/2015/04/a-radical-new-look-for-logarithms.html
12.5 Tattoos on Math
After a friend of mine got a tattoo with a representation of the cosecant function, it got me thinking about how there's another sense in which this function is a tattoo on math.------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted on new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: http://3b1b.co/recommendedVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3Blue1BrownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3Blue1Brown
12.6 Fractal charm: Space filling curves
A montage of space filling curves, meant as a supplement to the Hilbert curve video.
12.7 How to count to 1000 on two hands
Typically when we think of counting on two hands, we count up to 10, but fingers can contain much more information than that! This video shows how to think about counting in binary.
13 Recommended
13.1 Visualizing the Riemann hypothesis and analytic continuation
Unraveling an enigmatic function.Home page: https://www.3blue1brown.com/Brought to you by you: http://3b1b.co/zeta-thanksPosters/shirts for this visualization at http://3b1b.co/storeMusic by Vince Rubinetti: https://soundcloud.com/vincerubinetti/riemann-zeta-functionCheck out some of Vince's other work here: http://www.vincentrubinetti.com/For those who want to learn more about complex exponentiation, here are a few resources:- My video on the topic: http://youtu.be/mvmuCPvRoWQ- Mathologer's: https://youtu.be/-dhHrg-KbJ0- Better Explained: https://goo.gl/z28x2RFor those who want to learn more about the relationship between 1+2+3+4+... and -1/12, I'm quite fond of this blog post by Terry Tao: https://goo.gl/XRzyTJAlso, in a different video "What does it feel like to invent math", I give a completely different example of how adding up growing positive numbers can meaningfully give a negative number, so long as you loosen your understanding of what distance should mean for numbers: https://youtu.be/XFDM1ip5HdUInterestingly, that vertical line where the convergent portion of the function appears to abruptly stop corresponds to numbers whose real part is Euler's constant, ~0.577. For those who know what this is, it's kind of fun to puzzle about why this is the case.------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted about new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: https://goo.gl/WmnCQZVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3Blue1BrownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3Blue1Brown
13.2 Who cares about topology? (Inscribed rectangle problem)
An unsolved conjecture, and a clever topological solution to a weaker version of the question.Brought to you by you: http://3b1b.co/topology-thanksHome page: https://www.3blue1brown.com/This video is based on a proof from H. Vaughan, 1977.You can see it written up (as a single rather-dense paragraph) here:http://topo.math.auburn.edu/tp/reprints/v06/tp06107.pdf------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted about new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: https://www.youtube.com/playlist?list=PLZHQObOWTQDPHP40bzkb0TKLRPwQGAoC-Various social media stuffs:Twitter: https://twitter.com/3Blue1BrownFacebook: https://www.facebook.com/3blue1brown/Reddit: https://www.reddit.com/r/3Blue1Brown
13.3 Fractals are typically not self-similar
An explanation of fractal dimension.Home page: https://www.3blue1brown.com/Brought to you by you: http://3b1b.co/fractals-thanksAnd by Affirm: https://www.affirm.com/Music by Vince Rubinetti: https://soundcloud.com/vincerubinetti/riemann-zeta-functionOne technical note: It's possible to have fractals with an integer dimension. The example to have in mind is some *very* rough curve, which just so happens to achieve roughness level exactly 2. Slightly rough might be around 1.1-dimension; quite rough could be 1.5; but a very rough curve could get up to 2.0 (or more). A classic example of this is the boundary of the Mandelbrot set. The Sierpinski pyramid also has dimension 2 (try computing it!).The proper definition of a fractal, at least as Mandelbrot wrote it, is a shape whose "Hausdorff dimension" is greater than its "topological dimension". Hausdorff dimension is similar to the box-counting one I showed in this video, in some sense counting using balls instead of boxes, and it coincides with box-counting dimension in many cases. But it's more general, at the cost of being a bit harder to describe. Topological dimension is something that's always an integer, wherein (loosely speaking) curve-ish things are 1-dimensional, surface-ish things are two-dimensional, etc. For example, a Koch Curve has topological dimension 1, and Hausdorff dimension 1.262. A rough surface might have topological dimension 2, but fractal dimension 2.3. And if a curve with topological dimension 1 has a Hausdorff dimension that *happens* to be exactly 2, or 3, or 4, etc., it would be considered a fractal, even though it's fractal dimension is an integer.See Mandelbrot's book "The Fractal Geometry of Nature" for the full details and more examples.------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted about new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: https://www.youtube.com/playlist?list=PLZHQObOWTQDPHP40bzkb0TKLRPwQGAoC-Various social media stuffs:Twitter: https://twitter.com/3Blue1BrownFacebook: https://www.facebook.com/3blue1brown/Reddit: https://www.reddit.com/r/3Blue1Brown
13.4 Euler's formula with introductory group theory
Intuition for e^(pi i) = -1, and an intro to group theory.Home page: https://www.3blue1brown.com/Brought to you by you: http://3b1b.co/epii-thanksAnd by the Emerald Cloud Lab:- Application software engineer: http://3b1b.co/ecl-app-se- Infrastructure engineer: http://3b1b.co/ecl-infra-se- Lab focused engineer: http://3b1b.co/ecl-lab-se- Scientific computing engineer: http://3b1b.co/ecl-sci-compThere's a slight mistake at 13:33, where the angle should be arctan(1/2) = 26.565 degrees, not 30 degrees. Arg! If anyone asks, I was just...er...rounding to the nearest 10's.For those looking to read more into group theory, I'm a fan of Keith Conrad's expository papers: http://www.math.uconn.edu/~kconrad/blurbs/------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted about new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: http://3b1b.co/recommendedVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3Blue1BrownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3Blue1Brown
13.5 All possible pythagorean triples, visualized
The pythagorean triples like (3, 4, 5), (5, 12, 13), etc. all follow a nice pattern which complex numbers expose in a beautiful way.Brought to you by you: http://3b1b.co/triples-thanksHome page: https://www.3blue1brown.com/And by Remix: https://www.remix.com/jobsRegarding the brief reference to Fermat's Last Theorem, what should be emphasized is that it refers to *positive* integers. You can of course have things like 0^3 + 2^3 = 2^3, or (-3)^3 + 3^3 = 0^3. Music by Vincent Rubinetti: https://vincerubinetti.bandcamp.com/album/the-music-of-3blue1brown------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted about new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: http://3b1b.co/recommendedVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3Blue1BrownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3Blue1Brown
13.6 Pi hiding in prime regularities
A story of pi, primes, complex numbers, and how number theory braids them together.Brought to you by you: http://3b1b.co/leibniz-thanksHome page: https://www.3blue1brown.com/And by Remix: https://www.remix.com/The fact that only primes that are one above a multiple of four can be expressed as the sum of two squares is known as "Fermat's theorem on sums of two squares": https://goo.gl/EdhaN2Music by Vince Rubinetti:https://vincerubinetti.bandcamp.com/album/the-music-of-3blue1brown------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted about new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: http://3b1b.co/recommendedVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3Blue1BrownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3Blue1Brown
13.7 Hilbert's Curve: Is infinite math useful?
Space-filling curves, turning visual information into audio information, and the connection between infinite and finite math (this is a re-upload of an older video which had much worse audio).Supplement with more space-filling curve fun: https://youtu.be/RU0wScIj36oFor more information on sight-via sound, this paper involving rewiring a ferret's retinas to its auditory cortex is particularly thought-provoking: http://phy.ucsf.edu/~houde/coleman/sur2.pdfAlternatively, here is the NYT summary: https://goo.gl/qNuc14Also, check out this excellent podcast on Human echolocation: https://goo.gl/23f4YhFor anyone curious to read more about the connections between infinite and finite math, consider this Terry Tao blog post: https://goo.gl/NZ4yrWLion photo by Kevin PluckMusic by Vincent Rubinetti: https://vincerubinetti.bandcamp.com/album/the-music-of-3blue1brown------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted on new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: http://3b1b.co/recommendedVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3Blue1BrownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3Blue1Brownm/r/3Blue1Brown
13.8 What does it feel like to invent math?
An exploration of infinite sums, from convergent to divergent, including a brief introduction to the 2-adic metric, all themed on that cycle between discovery and invention in math.Home page: https://www.3blue1brown.com/Music: Legions (Reverie) by Zoe Keating------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted about new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: https://goo.gl/WmnCQZVarious social media stuffs:Patreon: https://www.patreon.com/3blue1brownTwitter: https://twitter.com/3Blue1BrownFacebook: https://www.facebook.com/3blue1brown/Reddit: https://www.reddit.com/r/3Blue1Brown
13.9 But how does bitcoin actually work?
The math behind cryptocurrencies.Home page: https://www.3blue1brown.com/Brought to you by you: http://3b1b.co/btc-thanksAnd by Protocol Labs: https://protocol.ai/join/Some people have asked if this channel accepts contributions in cryptocurrency form. As a matter of fact, it does:http://3b1b.co/crypto2^256 video: https://youtu.be/S9JGmA5_unYMusic by Vincent Rubinetti: https://soundcloud.com/vincerubinetti/heartbeatHere are a few other resources I'd recommend:Original Bitcoin paper: https://bitcoin.org/bitcoin.pdfBlock explorer: https://blockexplorer.com/Blog post by Michael Nielsen: https://goo.gl/BW1RV3(This is particularly good for understanding the details of what transactions look like, which is something this video did not cover)Video by CuriousInventor: https://youtu.be/Lx9zgZCMqXEVideo by Anders Brownworth: https://youtu.be/_160oMzblY8Ethereum white paper: https://goo.gl/XXZddT------------------Animations largely made using manim, a scrappy open source python library. https://github.com/3b1b/manimIf you want to check it out, I feel compelled to warn you that it's not the most well-documented tool, and has many other quirks you might expect in a library someone wrote with only their own use in mind.Music by Vincent Rubinetti.Download the music on Bandcamp:https://vincerubinetti.bandcamp.com/album/the-music-of-3blue1brownStream the music on Spotify:https://open.spotify.com/album/1dVyjwS8FBqXhRunaG5W5uIf you want to contribute translated subtitles or to help review those that have already been made by others and need approval, you can click the gear icon in the video and go to subtitles/cc, then "add subtitles/cc". I really appreciate those who do this, as it helps make the lessons accessible to more people.------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted on new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: http://3b1b.co/recommendedVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3Blue1BrownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3Blue1Brown
13.10 Thinking outside the 10-dimensional box
Visualizing high-dimensional spheres to understand a surprising puzzle.Home page: https://www.3blue1brown.com/Brought to you by you: http://3b1b.co/high-d-thanksAnd by Brilliant: https://brilliant.org/3b1bPodcast! https://www.benbenandblue.com/Check out Ben Eater's channel: https://www.youtube.com/user/eaterbc------------------Animations largely made using manim, a scrappy open source python library. https://github.com/3b1b/manimIf you want to check it out, I feel compelled to warn you that it's not the most well-documented tool, and it has many other quirks you might expect in a library someone wrote with only their own use in mind.Music by Vincent Rubinetti.Download the music on Bandcamp:https://vincerubinetti.bandcamp.com/album/the-music-of-3blue1brownStream the music on Spotify:https://open.spotify.com/album/1dVyjwS8FBqXhRunaG5W5uIf you want to contribute translated subtitles or to help review those that have already been made by others and need approval, you can click the gear icon in the video and go to subtitles/cc, then "add subtitles/cc". I really appreciate those who do this, as it helps make the lessons accessible to more people.------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted on new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: http://3b1b.co/recommendedVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3Blue1BrownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3Blue1Brown
13.11 Some light quantum mechanics (with minutephysics)
The math of superposition and quantum states.minutephysics channel: https://www.youtube.com/user/minutephysicsBrought to you by you: http://3b1b.co/light-quantum-thanksAnd by Brilliant: https://brilliant.org/3b1bHuge thanks to my friend Evan Miyazono, both for encouraging me to do this project, and for helping me understand many things along the way.This is a simple primer for how the math of quantum mechanics, specifically in the context of polarized light, relates to the math of classical waves, specifically classical electromagnetic waves.I will say, if you *do* want to go off and learn the math of quantum mechanics, you just can never have too much linear algebra, so check out the series I did at http://3b1b.co/essence-of-linear-algebraMistakes: As several astute commenters have pointed out, the force arrow is pointing the wrong way at 2:18. Thanks for the catch!*Note on conventions: Throughout this video, I use a single-headed right arrow to represent the horizontal direction. The standard in quantum mechanics is actually to use double-headed arrows for describing polarization states, while single-headed arrows are typically reserved for the context of spin.What's the difference? Well, using a double-headed arrow to represent the horizontal direction emphasizes that in a quantum mechanical context, there's no distinction between left and right. They each have the same measurable state: horizontal (e.g. they pass through horizontally oriented filters). Once you're in QM, these kets are typically vectors in a more abstract space where vectors are not necessarily spatial directions but instead represent any kind of state.Because of how I chose to motivate things with classical waves, where it makes sense for this arrow to represent a unit vector in the right direction, rather than the more abstract idea of a horizontal state vector, I chose to stick with the single-headed notation throughout, though this runs slightly against convention.Music by Vincent Rubinetti:https://vincerubinetti.bandcamp.com/album/the-music-of-3blue1brown------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted on new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: http://3b1b.co/recommendedVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3Blue1BrownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3Blue1Brown
13.12 The Brachistochrone, with Steven Strogatz
Steven Strogatz and I talk about a famous historical math problem, a clever solution, and a modern twist.------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted about new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: https://www.youtube.com/playlist?list=PLZHQObOWTQDPHP40bzkb0TKLRPwQGAoC-Various social media stuffs:Patreon: https://www.patreon.com/3blue1brownTwitter: https://twitter.com/3Blue1BrownFacebook: https://www.facebook.com/3blue1brown/Reddit: https://www.reddit.com/r/3Blue1Brown
13.13 Binary, Hanoi and Sierpinski, part 1
Binary counting can solve the towers of Hanoi puzzle, and if this isn't surprising enough, it can lead to a method for finding a curve that fills Sierpinski's triangle (which I get to in part 2).Thanks to Desmos for their help in supporting this video. They're hiring, and anyone interested should check out https://www.desmos.com/careersThanks to all Patreon supporters as well, you can support and get early access to future "Essence of" series here: https://www.patreon.com/3blue1brownI also want to give a special shoutout to the following patrons: CrypticSwarm, Ali Yahya, Dave Nicponski, Juan Batiz-Benet, Yu Jun, Othman Alikhan, Markus Persson, Joseph John Cox, Luc Ritchie, Einar Wikheim Johansen, Rish Kundalia, Achille Brighton, Kirk Werklund, Ripta Pasay, Felipe Diniz, Chris, Curtis Mitchell, Ari Royce, Bright , Myles Buckley, Robert P Zuckett, Andy Petsch, Otavio good, Karthik T, Steve Muench, Viesulas Sliupas, Steffen Persch, Brendan Shah, Andrew Mcnab, Matt Parlmer, Naoki Orai, Dan Davison, Jose Oscar Mur-Miranda, Aidan Boneham, Brent Kennedy, Henry Reich, Sean Bibby, Paul Constantine, Justin Clark, Mohannad Elhamod, Denis, Ben Granger, Jeffrey Herman, Jacob Young.
13.14 Binary, Hanoi, and Sierpinski, part 2
After seeing how binary counting can solve the towers of Hanoi puzzle in the last video, here we see how ternary counting solve a constrained version of the puzzle, and how this gives a way to walk through a Sierpinski triangle graph structure.Thanks to Desmos for their help in supporting this video. They're hiring, and anyone interested should check out https://www.desmos.com/careersThanks to all Patreon supporters as well, you can support and get early access to future "Essence of" series here: https://www.patreon.com/3blue1brownI also want to give a special shoutout to the following patrons: CrypticSwarm, Ali Yahya, Dave Nicponski, Juan Batiz-Benet, Yu Jun, Othman Alikhan, Markus Persson, Joseph John Cox, Luc Ritchie, Einar Wikheim Johansen, Rish Kundalia, Achille Brighton, Kirk Werklund, Ripta Pasay, Felipe Diniz, Chris, Curtis Mitchell, Ari Royce, Bright , Myles Buckley, Robert P Zuckett, Andy Petsch, Otavio good, Karthik T, Steve Muench, Viesulas Sliupas, Steffen Persch, Brendan Shah, Andrew Mcnab, Matt Parlmer, Naoki Orai, Dan Davison, Jose Oscar Mur-Miranda, Aidan Boneham, Brent Kennedy, Henry Reich, Sean Bibby, Paul Constantine, Justin Clark, Mohannad Elhamod, Denis, Ben Granger, Jeffrey Herman, Jacob Young.
13.15 Music And Measure Theory
A connection between a classical puzzle about rational numbers and what makes music harmonious.
13.16 Circle Division Solution
An explanation of a neat circle puzzle involving combinatorics, graphs, Euler's characteristic formula and pascal's triangle.Typo: At 7:30, the second term at the very bottom should have "k-1" instead of "k"Music: Wyoming 307 by Time for Three
13.17 Euler's Formula and Graph Duality
A description of planar graph duality, and how it can be applied in a particularly elegant proof of Euler's Characteristic Formula.Music: Wyoming 307 by Time For Three
14 Brachistochrone
14.1 The Brachistochrone, with Steven Strogatz
Steven Strogatz and I talk about a famous historical math problem, a clever solution, and a modern twist.------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted about new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: https://www.youtube.com/playlist?list=PLZHQObOWTQDPHP40bzkb0TKLRPwQGAoC-Various social media stuffs:Patreon: https://www.patreon.com/3blue1brownTwitter: https://twitter.com/3Blue1BrownFacebook: https://www.facebook.com/3blue1brown/Reddit: https://www.reddit.com/r/3Blue1Brown
14.2 Snell's law proof using springs
This is a supplement to the Brachistochrone video, proving Snell's law with a clever little argument by Mark Levi.
15 Space filling curves
15.1 Fractal charm: Space filling curves
A montage of space filling curves, meant as a supplement to the Hilbert curve video.
15.2 Hilbert's Curve: Is infinite math useful?
Space-filling curves, turning visual information into audio information, and the connection between infinite and finite math (this is a re-upload of an older video which had much worse audio).Supplement with more space-filling curve fun: https://youtu.be/RU0wScIj36oFor more information on sight-via sound, this paper involving rewiring a ferret's retinas to its auditory cortex is particularly thought-provoking: http://phy.ucsf.edu/~houde/coleman/sur2.pdfAlternatively, here is the NYT summary: https://goo.gl/qNuc14Also, check out this excellent podcast on Human echolocation: https://goo.gl/23f4YhFor anyone curious to read more about the connections between infinite and finite math, consider this Terry Tao blog post: https://goo.gl/NZ4yrWLion photo by Kevin PluckMusic by Vincent Rubinetti: https://vincerubinetti.bandcamp.com/album/the-music-of-3blue1brown------------------3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted on new videos, subscribe, and click the bell to receive notifications (if you're into that).If you are new to this channel and want to see more, a good place to start is this playlist: http://3b1b.co/recommendedVarious social media stuffs:Website: https://www.3blue1brown.comTwitter: https://twitter.com/3Blue1BrownPatreon: https://patreon.com/3blue1brownFacebook: https://www.facebook.com/3blue1brownReddit: https://www.reddit.com/r/3Blue1Brownm/r/3Blue1Brown
16 Moser Circle Problem
16.1 A Curious Pattern Indeed
A teaser for some future videos regarding a pattern which lures an unsuspecting doodler into thinking it will be powers of two.
16.2 Circle Division Solution
An explanation of a neat circle puzzle involving combinatorics, graphs, Euler's characteristic formula and pascal's triangle.Typo: At 7:30, the second term at the very bottom should have "k-1" instead of "k"Music: Wyoming 307 by Time for Three
16.3 Euler's Formula and Graph Duality
A description of planar graph duality, and how it can be applied in a particularly elegant proof of Euler's Characteristic Formula.Music: Wyoming 307 by Time For Three