二分图最大匹配算法

我觉得链接文章写得非常好，看这一篇就足够了。匈牙利算法的本质思想，还是不断地寻找增广路径。对于网络最大流问题来说，增广路径就是在残留图上寻找s->t的可行路径，而对于二分图来说，增广路径是 "一条s,t分别是未匹配节点，中间所经过的节点都是匹配节点的路径"。

以下图为例，9->4->8->1->6->2就是一条增广路径

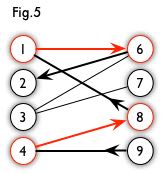
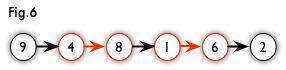
(4,8),(1,6)是匹配节点
利用增广路径的话，我们可以增加一对匹配节点（多一条匹配边）
修改后匹配节点为 (9,4), (8,1), (6,2).

在算法最外层，我们需要遍历所有“未匹配”的节点，所以外层循环时间复杂度是O(V). 寻找增广路径的时间复杂度则是O(E). 所以总体时间复杂度是O(VE). 我的算法(BFS版本)在实现上和链接文章的里面给的实现有点不同，一个差别是将处理增广路径单独分离出来，另外一个差别就是增广路径的表示我觉得会更加清晰一些。另外我的实现中顶点编号从1开始。

def hungarian(adj):
    n = len(adj)
    matching = [0] * n
    check = [0] * n
    parent = [0] * n
    from collections import deque
    dq = deque()

    for t in range(1, n):
        if matching[t] != 0: continue

        dq.clear()
        dq.append(t)
        check[t] = t
        parent[t] = 0
        ending = 0
        while dq and ending == 0:
            u = dq.popleft()
            for v in adj[u]:
                if check[v] == t: continue
                check[v] = t
                parent[v] = u
                if matching[v] == 0:
                    ending = v
                    break
                else:
                    parent[matching[v]] = v
                    dq.append(matching[v])

        # found a augmented path.
        # ending -> p[ending] -> .. x -> t -> 0
        path = []
        while ending != 0:
            p = parent[ending]
            path.append(ending)
            path.append(p)
            matching[ending] = p
            matching[p] = ending
            ending = parent[p]
        path = path[::-1]
        print('augpath', path)
    return matching