alpha-beta剪枝技术

https://en.wikipedia.org/wiki/Alpha%E2%80%93beta_pruning

AB剪枝是基于min-max搜索策略的优化方法，原理就是根据上层已知的值来减少树的搜索。

注意我们这里必须以一致视角来eval game state. 比如下棋，在我方下完之后，就需要评估我方的局面，所以我们希望找到极大值。 在对方下完之后，也必须评估我方的局面，所以对方肯定希望找到我们的极小值。这样有两个好处，一个是max-min搜索和ab剪枝， 另外一方面到了叶子节点上评估函数是一致的. 如果我方是黑棋的话，那么我们始终只需要评估当前棋盘上黑棋的价值。

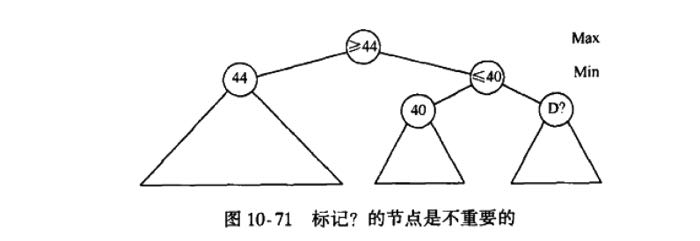
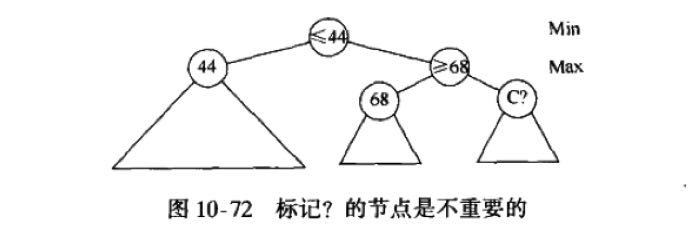
参考下面代码的话，10-71对应的剪枝是alpha cut-off, 10-72对应的是beta cut-off.

Pasted-Image-20231225104723.png Pasted-Image-20231225104646.png 

function alphabeta(node, depth, α, β, maximizingPlayer) is
    if depth = 0 or node is a terminal node then
        return the heuristic value of node
    if maximizingPlayer then
        value := −∞
        for each child of node do
            value := max(value, alphabeta(child, depth − 1, α, β, FALSE))
            α := max(α, value)
            if α ≥ β then
                break (* β cut-off *)
        return value
    else
        value := +∞
        for each child of node do
            value := min(value, alphabeta(child, depth − 1, α, β, TRUE))
            β := min(β, value)
            if α ≥ β then
                break (* α cut-off *)
        return value

(* Initial call *)
alphabeta(origin, depth, −∞, +∞, TRUE)

我考虑了一下觉得alpha, beta可以缩减成为一个变量，但是不确定是否正确 

function alphabeta(node, depth, threshold, maximizingPlayer) is
    if depth = 0 or node is a terminal node then
        return the heuristic value of node
    if maximizingPlayer then
        value := −∞
        for each child of node do
            value := max(value, alphabeta(child, depth − 1, value, FALSE))
            if value >= thresold then
                break (* β cut-off *)
        return value
    else
        value := +∞
        for each child of node do
            value := min(value, alphabeta(child, depth − 1, value, TRUE))
            if threshold >= value then
                break (* α cut-off *)
        return value

alphabeta(origin, depth, +∞, True)